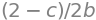Introducción a SymPy

`SymPy es una librería para Python de matemática simbólica. Para poder usarlo necesitamos importar el paquete SymPy.

import sympy as sp

Para imprimir las fórmulas por pantalla y obtener una visualización tipográfica agradable, además es necesario ejecutar:

sp.init_printing()

Tenga en cuenta que esto puede cambiar según cual sea de la versión de sympy

Luego, ya para comenzar con la operatorio simbólica, necesitamos crear un símbolo.

x = sp.Symbol('x')
x

SymPy nos permite hacer muchas operaciones matemáticas que serían tediosas a mano. Por ejemplo, podemos expandir un polinomio:

polynomial = (2*x + 3)**4
polynomial.expand()

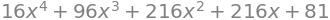
Observe lo que sucedió: definimos un nuevo nombre llamado polynomial y luego usamos el método .expand() para expandir el polinomio. Podemos ver todos los métodos asociados con un objeto escribiendo su nombre y un punto y luego presionando «tabulador».

Acceda a la lista de métodos para la variable polynomial ingresando «.» y presionando tabulador al final de la línea en la celda a continuación.

Para obtener ayuda sobre cualquier método, podemos escribir su nombre y agregar un ? al final, luego evaluar la celda.

Obtenga ayuda sobre el método .expand() mediante la evaluación de la celda a continuación:

polynomial.expand?

También es posible obtener ayuda para una función colocando el cursor entre los paréntesis y presionando Mayúscula + Tabulador

Por supuesto, también podemos factorizar polinomios:

(x**2 + 2*x + 1).factor()

Cálculo

SymPy sabe integrar y diferenciar.

polynomial.diff(x)  # First derivative

polynomial.diff(x, 2)  # Second derivative

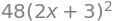
# indefinite integral - note no constant of integration is added
polynomial.integrate(x)

# Note that integrate takes one argument which is a tuple for the definite
# integral
polynomial.integrate((x, 1, 2))

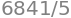
Límites

Podemos evaluar los límites usando SymPy, incluso para límites «interesantes» donde necesitaríamos la regla de L’Hopital

sp.limit((2*sp.sin(x) - sp.sin(2*x))/(x - sp.sin(x)), x, 0)

Aproximación

SymPy tiene soporte incorporado para la expansión de series de Taylor

nonlinear_expression = sp.sin(x)

# taylor expansion in terms of the x variable, around x=2, first order.
sp.series(nonlinear_expression, x, 2, 2)

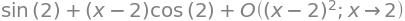
Para eliminar el término de perdida use .removeO()

temp = sp.series(nonlinear_expression, x, 2, 2)
temp.removeO()

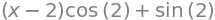
También notará que el comportamiento predeterminado de SymPy es retener representaciones exactas de ciertos números:

number = sp.sqrt(2)*sp.pi
number

Para convertir las representaciones exactas de arriba en representaciones aproximadas de punto flotante, use uno de estos métodos:

• sympy.N funciona con expresiones complicadas que también contienen variables.

• float devolverá un número de tipo float de Python normal y es útil cuando se interactúa con programas que no son de SymPy.

sp.N(number*x)

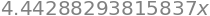
float(number)

Resolver ecuaciones

SymPy puede ayudarnos a resolver y manipular ecuaciones utilizando la función solve. Como muchas funciones de resolución, encuentra ceros de una función, por lo que tenemos que reescribir las ecuaciones de igualdad para que sean iguales a cero,

\[\begin{split} \begin{aligned} 2x^2 + 2 &= 4 \\ 2x^2 + 2 - 4 &= 0 \end{aligned} \end{split}\]

solutions = sp.solve(2*x**2 + 2 - 4)
solutions

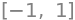
solutions[0]

También podemos usar sp.Eq para construir ecuaciones

equation = sp.Eq(2*x**2 + 2, 4)
equation

La función roots nos dará también la multiplicidad de las raíces.

sol = sp.roots(equation)
sol

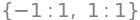
Esto no dice que la ecuación anterior tiene una solución -1 y otra solución igual 1.

También podemos resolver sistemas de ecuaciones pasando una lista de ecuaciones para resolver y pidiendo una lista de variables para resolver.

x, y = sp.symbols('x, y')
sp.solve([x + y - 2,
          x - y - 0], [y, x])

Esto incluso funciona con variables simbólicas en las ecuaciones.

a, b, c = sp.var('a, b, c')
solution = sp.solve([a*x + b*y - 2,
                     a*x - b*y - c], [x, y])
solution

solution.items()

dict_items([(x, (c + 2)/(2*a)), (y, (2 - c)/(2*b))])

a = [i for i in solution.values()]

a[0]

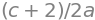
a[1]