Compensadores de adelanto y de retraso de fase

Controlar un sistema dado es establecer en su funcionamiento de acuerdo con unos requisitos o especificaciones. En este capítulo se analizan los cambios que se pueden lograr en un dispositivo al añadir un nuevo polo y un nuevo cero al sistema, que se introduce en un lazo de control.

Estos nuevos elementos no tienen por qué ser de las mismas características que la planta. Si la planta es un sistema mecánico, el controlador puede estar constituido por nuevos elementos mecánicos o un dispositivo eléctrico. La implementación final del compensador no importa mientras su función de transferencia, la ecuación diferencial que gobierna su comportamiento, sea la misma.

Se puede definir compensación como la modificación de la dinámica de un sistema para cumplir unas especificaciones determinadas.

Generalidades

El compensador objeto de estudio en este capítulo actúa sobre la planta en función del error que existe entre la salida del sistema y la referencia que se desea seguir como se ve la figura siguiente, y posee una función de transferencia con una ganancia, un polo y un cero.

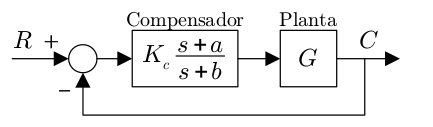
Figura 96 Compensador polo-cero

Con estos presupuestos, se da por supuesto que el sistema se controla con un lazo de realimentación negativa unitaria. Sin embargo, en ocasiones pueden diseñarse compensadores que se coloquen en otras posiciones del lazo de control, resultando una realimentación negativa no unitaria. Este tipo de compensadores no se estudiarán en la presente asignatura.

Especificaciones

Las especificaciones exigibles a un sistema pueden ser de muy distinta índole. Habitualmente se clasifican como restricciones del sistema en el dominio temporal:

• Régimen transitorio: tiempo de establecimiento, tiempo de crecimiento, tiempo de pico, sobrevalor máximo, ancho de banda, etc.

• Régimen permanente: error nulo o limitado ante un tipo determinado de entrada, rechazo a las perturbaciones, etc.

Tipos de compensación

Es posible lograr que un sistema cumpla una serie de especificaciones con distintos compensadores. Una posible clasificación para los tipos de compensador puede ser:

• Compensador de adelanto de fase. El cero produce un adelanto de fase a bajas frecuencias respecto el polo. El resultado final es que el compensador adelanta fase en un determinado rango de frecuencias.

• Compensador de retraso de fase. En este caso el polo produce un retraso de fase a más bajas frecuencias respecto el cero. El resultado final es que el compensador retrasa fase en un determinado rango de frecuencias.

• Compensador de adelanto-retraso de fase. el compensador consiste el producto de las funciones de transferencia de un compensador de adelanto de fase y uno de retraso. El compensador de retraso se coloca a menores frecuencias que el de adelanto.

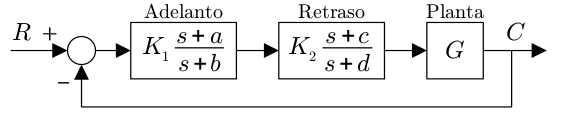
Figura 97 Compensador adelanto-atraso

Método de ajuste por lugar de las raíces

En el plano \(s\) se añade el nuevo polo y cero del compensador. Se modifica el lugar de las raíces del sistema de forma que los polos dominantes de la planta en lazo cerrado queden ubicados donde se desee.

Compensador de adelanto de fase

Un compensador de adelanto de fase tiene la siguiente expresión:

\[D(s)=K\frac{1+Ts}{1+\alpha T s}=\frac{K}{\alpha}\frac{s+\frac{1}{T}}{s+\frac{1}{\alpha T}}=K_c\frac{s+a}{s+b}\]

con \(0<\alpha<1\) y \(a<b\).

La primera expresión es más útil cuando se trabaja en el diagrama de Bode, mientras que la segunda es preferible cuando se trabaja en el lugar de las raíces. En los siguientes apartados se explicarán los procedimientos de ajuste de los tres parámetros del compensador. Para todos los métodos se usará siempre el mismo ejemplo de la figura siguiente:

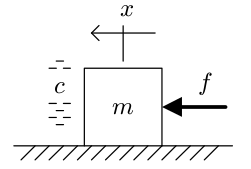
Figura 98 Sistema a compensar

Se trata de un sistema mecánico en el que un actuador mueve una compuerta de masa \(m\) dentro de un medio con viscosidad \(c\). El actuador debe colocar la compuerta siguiendo la referencia de posición que se le comande de tal forma que el tiempo de establecimiento sea menor o igual que 2 segundos y que el sobrevalor máximo respecto la referencia sea del 20% o menor. La masa de la compuerta es de 0.25 kg y el coeficiente viscoso es 0.5 Ns/m.

La función de transferencia que relaciona la fuerza \(f\) aplicada a la masa y su desplazamiento, sustituyendo también los valores numéricos se ve en la siguiente expresión:

\[G(s)=\frac{1}{ms^2+cs}=\frac{4}{s(s+2)}\]

Ajuste por lugar de las raíces

La introducción de un polo y un cero en el sistema puede beneficiar al régimen transitorio, es decir, puede hace el sistema más rápido si el nuevo cero está más cerca del origen que el nuevo polo. En ese caso, las ramas del lugar de las raíces se alejan del eje imaginario del plano \(S\). Por tanto, se puede elegir una ganancia para el sistema que deje los polos dominantes del sistema con un tiempo de establecimiento menor.

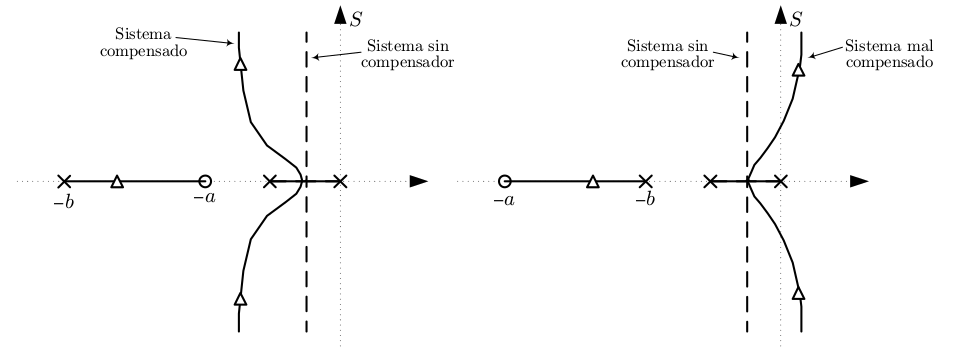
Figura 99 Efecto de un polo en lugar de las raíces

Este efecto se muestra cualitativamente en la figura anterior justifica la definición del compensador de adelanto de fase donde se decía \(a < b\). Evidentemente, la localización de polo y del cero del compensador dependerá de cuánto se quiera alejar las ramas del lugar de las raíces del eje imaginario. Son las especificaciones que se deseen conseguir las que van a marcar la separación relativa del nuevo polo y cero. Resulta casi inmediato, a partir de los requerimientos de tiempo de establecimiento y sobrevalor calcular los polos dominantes objeto del diseño.

\[\begin{split} \begin{eqnarray} M_p<0.2 & \implies \zeta \ge 0.45, &\text{se elije }\zeta=0.5\\ t_s<2\text{seg} & \implies \omega_n \ge 4\text{rad/s}, &\text{se elije }\omega_n=4\text{rad/s}\\ p_{\Delta}&=-\zeta\omega_n\pm\omega_n\sqrt{1-\zeta^2}j&=-2\pm 3.46j \end{eqnarray} \end{split}\]

Con el valor de sobrevalor se elige un valor para el amortiguamiento de los polos objetivo, primer ecuación de las tres anteriores, y con éste y el tiempo de establecimiento se calcula la frecuencia natural.

La posición final de los polos objetivo, depende de las elecciones que haya realizado el ingeniero. Es difícil que dos ingenieros obtengan exactamente la misma solución numérica para un mismo problema. Por tanto, las soluciones que se proponen en estos apuntes no son las únicas que se pueden dar correctamente para cada problema.

Obtenida la localización de los polos objetivo, se aplica en ese punto la condición del ángulo. Esto se realiza precisamente porque se quiere garantizar que esos puntos pertenecen al nuevo lugar de las raíces del sistema.

Evidentemente, la condición del ángulo se debe aplicar teniendo en cuenta el nuevo polo y cero que introduce el compensador, cuya posición todavía está por determinar, ver la figura siguiente:

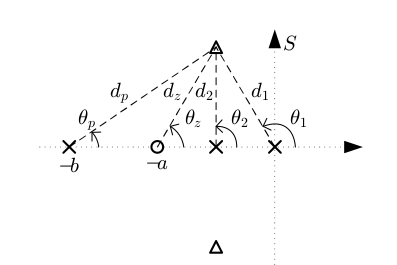
Figura 100 Ángulos y distancias vistas al polo objetivo

\[\sum_{i=1}^m \hat{z_ip_\Delta}-\hat{z_jp_\Delta}=\theta_z-\theta_p-\theta_1-\theta_2=\phi_c-\theta_1-\theta_2 = -180\]

En la ecuación anterior los ángulos vistos desde los polos o ceros de la planta son conocidos. La única incógnita es la diferencia de ángulos del cero y polo del compensador. A esa diferencia se le llamará \(\phi_c\) y es el ángulo con que el polo objetivo “ve” al polo y cero del compensador. Cualquier pareja polo-cero que el polo objetivo vea con el mismo ángulo \(\phi_c\) es una posible solución al problema.

\[\phi_c =-180^0+\theta_1+\theta_2= -180^0+120^0+90^0=30^0\]

En el caso concreto del ejemplo \(\phi_c\) vale \(30^0\). Siempre que se trate de un compensador de adelanto de fase este ángulo debe dar positivo, ya que el cero está más cercano al origen y verá al polo objetivo con mayor ángulo que el polo del compensador. Cualquier pareja polo-cero que sea vista por el polo objetivo con 30\(^0\) es una hipotética solución al problema.

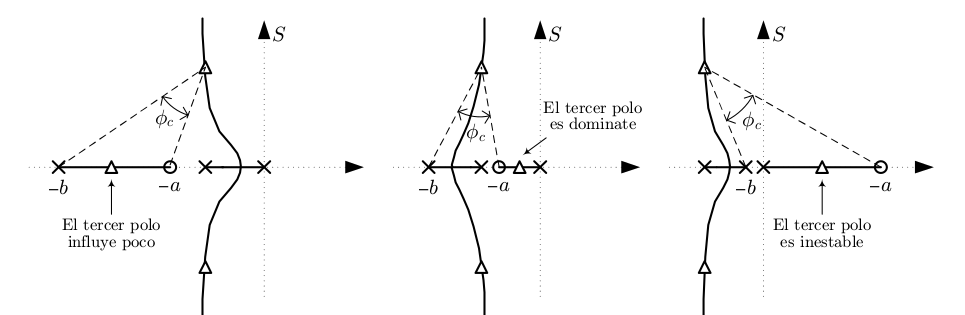
Figura 101 Posiciones del par polo-cero posibles del compensador

Sin embargo, la elección de la posición del par polo-cero no es absolutamente arbitraria. Efectivamente se puede conseguir que el lugar de las raíces pase por el polo objetivo, pero puede ser que en la configuración final del sistema, el polo dominante sea otro. Esta posibilidad hay que evitarla. Si se busca que el régimen transitorio lo caracterice la posición de los polos objetivo, éstos deben quedar como dominantes del sistema.

Incluso es posible colocar el par polo-cero en la zona del plano \(S\) de parte real positiva y cumplir el deseo de que el polo objetivo pertenezca al lugar de las raíces, pero dejar el tercer polo del sistema de forma que lo hace inestable. En conclusión, la posición del polo y del cero del compensador es libre mientras el polo objetivo los vea con el ángulo \(\phi_c\) adecuado y éstos queden como dominantes del sistema.

Dejando claro que el ingeniero puede elegir la posición del polo y del cero del compensador, cumpliendo lo que se ha enunciado en el párrafo anterior, en los siguientes apartados se explican algunos criterios que se han propuesto para su colocación. Dependiendo de la planta es posible que alguno de los criterios sea inviable o no consiga que el polo objetivo quede dominante en el sistema compensado. Siempre habrá que comprobar este último extremo, aunque sea de forma cualitativa.

En cuanto al cálculo de la ganancia del compensador, se debe aplicar la condición del módulo en el polo objetivo empleando lógicamente la posición del polo y el cero del compensador que se haya elegido.

\[K_cK_{la}=\frac{\prod_{j=1}^n \overline{p_jp_\Delta}}{\prod_{i=1}^m\overline{z_ip_\Delta}}=\frac{d_1d_2d_p}{d_z}\]

La única incógnita de la ecuación anterior es la ganancia \(K_c\) del compensador. En el ejemplo, la ganancia \(K\) la de la planta en lazo abierto expresando los polos y ceros en monomios es 4, la distancia \(d_1\) es 4, la distancia \(d_2\) es 3.46 y las distancias \(d_z\) y \(d_p\) se miden en el lugar de las raíces y dependen de la posición elegida para el polo y el cero del compensador.

Criterio de la bisectriz (opcional)

La posición del polo y del cero del compensador se elige centrándolos sobre la bisectriz del arco que forma la recta que une el polo objetivo con el origen del plano \(S\), y una recta horizontal que pasa por el polo objetivo, como se ve en la siguiente figura:

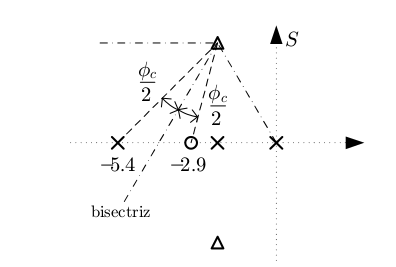
Figura 102 Criterio de la bisectriz

En el ejemplo propuesto, el polo del compensador queda aproximadamente en −5.4 y el cero en −2.9. Al aplicar la condición del módulo en el polo objetivo, la ganancia del compensador resulta ser aproximadamente 4.7, por tanto, el compensador tiene la siguiente expresión:

\[D(s)=4.7\frac{s+2.9}{s+5.4}\]

Se puede observar en la figura anterior que en el caso del ejemplo, este criterio no hubiera sido recomendable si el ángulo \(\phi_c\) hubiera sido mayor que 60\(^0\) . Si así fuera, el cero del compensador quedaría entre los dos polos de la planta y el lugar de las raíces tendría un tercer polo real en lazo cerrado más dominante que los polos objetivo.

Criterio de anular el segundo polo dominante (muy útil y fácil)

El cero del compensador se sitúa sobre el segundo polo dominante de la planta en lazo abierto y el polo donde quede, manteniendo el ángulo \(\phi_c\). El resultado es un sistema compensado con igual número de polos que sin compensar: no aparece ningún polo nuevo.

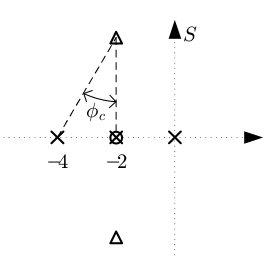
Figura 103 Criterio segundo polo dominante

En el ejemplo propuesto, el cero del compensador queda en −2 y el cero en −4. Al aplicar la condición del módulo en el polo objetivo, la ganancia del compensador resulta ser 4, por tanto, el compensador tiene la siguiente expresión:

\[D(s)=\frac{s+2}{s+4}\]

La limitación de uso de este criterio dependerá evidentemente de la posición del segundo polo dominante de la planta en lazo abierto. En el caso del ejemplo, este criterio no se puede emplear para un ángulo \(\phi_c\) mayor que 90\(^0\).

Criterio del cero bajo el polo objetivo (sencillo)

El cero del compensador se sitúa justo debajo del polo objetivo y el polo donde quede, manteniendo el ángulo \(\phi_c\). En este ejemplo, el resultado es el mismo que en el apartado anterior, porque ha coincidido que el segundo polo dominante de la planta en lazo abierto queda debajo del polo objetivo. Sin embargo, lo habitual es que den resultados distintos.

Este método se puede emplear sólo en el caso de que queden a la derecha del cero del compensador al menos dos polos de la planta en lazo abierto. Se puede observar en la figura anterior que el ejemplo se encuentra en el caso límite de uso, ya que si el segundo polo de la planta hubiese estado más a la izquierda, el tercer polo en lazo cerrado del sistema quedaría más dominante que los polos objetivo.

Si se cumple lo dicho en el párrafo anterior, para cualquier planta que se desee compensar, este criterio se puede emplear siempre que el ángulo \(\phi_c\) sea igual o menor que 90\(^0\).

Criterio de un compensador proporcional-derivativo (IMPORTANTE)

El polo del compensador se sitúa en el \(−\infty\) del plano \(S\) y el cero del compensador donde quede, manteniendo el ángulo \(\phi_c\). El compensador, por tanto, está compuesto por un único cero y ningún polo, (ver la figura siguiente).

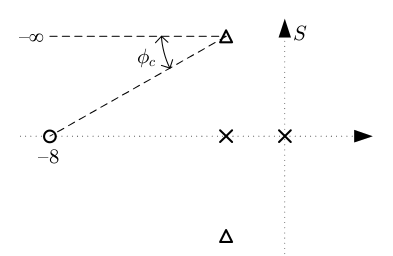
Figura 104 Criterio de un compensador proporcional-derivativo

El ángulo \(\phi_c\) coincide exactamente con el ángulo del que ve el cero al polo objetivo. En el ejemplo propuesto, el cero del compensador queda en −8 y la ganancia resulta ser 0.5, por tanto, el compensador tiene la siguiente expresión:

\[D(s)=0.5(s+8)\]

Este criterio, como la anulación de un polo de la planta en lazo abierto, no añade ningún polo nuevo en el sistema en lazo cerrado. El nombre de compensador proporcional-derivativo es coherente si se calcula en el dominio del tiempo cuál es la actuación sobre la planta \(u(t)\) en función del error \(e(t)\) de la ecuación siguiente donde se observa que hay una componente proporcional al error y otra proporcional a la derivada del error.

\[U(s)=K_c(s+a)E(s)=K_cE(s)+aK_cE(s)\xrightarrow{\mathcal{L}^{-1}}u(t)=K_c\frac{de(t)}{dt}+aK_ce(t)\]

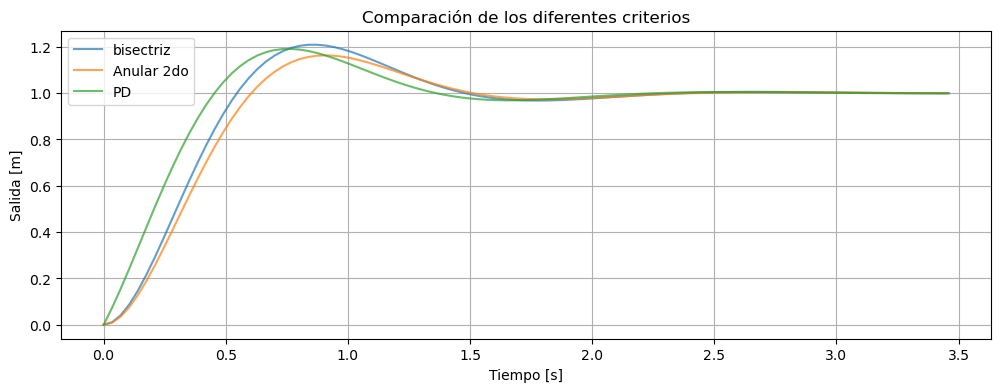
Comparación de la respuesta temporal de los distintos criterios (IMPORTANTE)

Resulta interesante comparar la respuesta temporal que consiguen los distintos criterios que se han enunciado. En la figura siguiente se nuestra la respuesta ante una entrada escalón unidad del sistema en lazo cerrado con los distintos compensadores que se han ido calculando.

Evidentemente, todos los compensadores consiguen cumplir las especificaciones de partida: tiempo de establecimiento menor que 2 segundos y sobrevalor del orden del 20 %. El compensador PD es fácilmente reconocible porque la pendiente inicial no es nula. El compensador del criterio de la bisectriz es un poco más rápido que el que anula el polo de la planta porque tiene la influencia del cero del compensador — también por eso tiene un poco más de sobrevalor.

Antes de continuar, conviene señalar que el método del lugar de las raíces que se ha descrito no permite el cumplimiento de especificaciones de error en régimen permanente. Los parámetros \(K_c\) , \(a\) y \(b\) del compensador se emplean para localizar los polos del sistema en lazo cerrado. Por tanto sólo puede lograr especificaciones de régimen transitorio.

Ha quedado patente en el ejemplo que se ha empleado que existe más de un compensador válido para unas especificaciones dadas. Sin embargo, a la hora de resolver un problema hay que decir explícitamente qué elecciones se están tomando en cada momento de forma justificada.

Se puede diseñar el compensador sin llegar a dibujar exactamente el lugar de las raíces del sistema, compensado o no, porque todas las operaciones se hacen con la posición de los polos y ceros de la planta y compensador en lazo abierto. El único punto que se conoce de forma exacta del lugar de las raíces puede ser el polo objetivo. Sin embargo, es muy conveniente al menos imaginar cómo va a quedar el lugar de las raíces del sistema compensado, de forma cualitativa.

Siempre que se pretendan mejorar el régimen transitorio, en el sentido de hacer el sistema más rápido de lo que de suyo es, el ángulo \(\phi_c\) va a dar positivo. Si da un ángulo pequeño, por ejemplo menos de 10\(^0\), significa que el lugar de las raíces del sistema sin compensador pasa bastante cerca de los polos objetivo. En este caso, es suficiente con diseñar un compensador puramente proporcional que deje los polo en lazo cerrado lo más cerca posible de los polos objetivo.

Si \(\phi_c\) da un ángulo muy grande, por ejemplo mayor que 70\(^0\), significa que el polo objetivo queda muy lejos del lugar de las raíces del sistema sin compensador. Quizá se pueden modificar las elecciones realizadas para el cálculo de los polos objetivo para que de un ángulo algo menor. Si no es así, no es recomendable elegir el compensador de adelanto de fase para cumplir las especificaciones exigidas. Habría que ir a otro tipo de controlador o afirmar que no se pueden cumplir dichas especificaciones.

import control as ctrl
import numpy as np
import matplotlib.pyplot as plt

G=ctrl.tf([4],[1, 2, 0])
po=-2+3.46j

D1=4.7*ctrl.tf([1,2.9],[1,5.4])
D2=4*ctrl.tf([1,2],[1,4])
D3=0.5*ctrl.tf([1,8],[1])

T1=ctrl.feedback(G*D1,1)
T2=ctrl.feedback(G*D2,1)
T3=ctrl.feedback(G*D3,1)

t1,y1=ctrl.step_response(T1)
t2,y2=ctrl.step_response(T2)
t3,y3=ctrl.step_response(T3)

Show code cell source Hide code cell source

fig, ax=plt.subplots(figsize=(12,4))
ax.set_title("Comparación de los diferentes criterios")
ax.plot(t1,y1, alpha=0.7, label="bisectriz")
ax.plot(t2,y2, alpha=0.7, label="Anular 2do")
ax.plot(t3,y3, alpha=0.7, label="PD")
ax.grid()
ax.set_xlabel('Tiempo [s]')
ax.set_ylabel('Salida [m]')
ax.legend();

Compensador por retraso de fase

Un compensador de retraso de fase tiene la siguiente forma:

\[D(s)=K\frac{1+Ts}{1+\beta Ts}= \frac{K}{\beta}\frac{s+\frac{1}{T}}{s+\frac{1}{\beta T}}=K_c\frac{s+a}{s+b}\]

con \(\beta>1\), y \(a>b\)

La primera expresión es más útil cuando se trabaja en el diagrama de Bode, mientras que la última es preferible cuando se trabaja en el lugar de las raíces.

Compensador que mejora el error

Un compensador de retraso de fase puede utilizarse para disminuir el error en régimen permanente sin empeorar el régimen transitorio del sistema. Haciendo \(K\) igual a \(\beta\) la ganancia y fase del compensador valen ambos 0 para altas frecuencias y por tanto no se modifica notoriamente el lugar de las raíces de la planta. Sin embargo, a bajas frecuencias se produce un aumento de ganancia, por lo que aumenta el coeficiente de error del sistema y por tanto disminuye el error del mismo.

\[D(s)=\beta\frac{1+Ts}{1+\beta Ts}= \frac{s+\frac{1}{T}}{s+\frac{1}{\beta T}}=\frac{s+a}{s+b}\]

Si se emplea el compensador de retraso de fase exclusivamente para disminuir el error en régimen transitorio, lo único que hay que hacer es: calcular \(\beta\) con la expresión siguiente

\[K_P=\lim_{s\rightarrow 0}\beta\frac{1+Ts}{1+\beta Ts}G(s)=\beta G(0)\]

igualar la ganancia \(K\) a \(\beta\) para que el compensador no modifique el lugar de las raíces y elegir \(T\) de tal forma que el cero del compensador quede entre una década y una octava antes del \(\omega_n\) de los polos objetivos. Esto último se hace para asegurar precisamente que el compensador no modifica el lugar de las raíces en la zona del transitorio.

Compensador de retraso que anula el error o compensador proporcional-integral

Se trata de la misma idea que en el apartado anterior, pero en lugar de disminuir el error del sistema, se anula. Para ello se incrementa el tipo del sistema en una unidad, haciendo que el polo del compensador se sitúe en el origen del plano \(S\).

\[D(s)=\frac{1+Ts}{Ts}=\frac{s+\frac{1}{T}}{s}=\frac{s+a}{s}\]

Este tipo de compensador se llama proporcional-integral porque en el dominio del tiempo la actuación en la planta es la suma de una parte proporcional al error y otra proporcional a la integral del error.

\[U(s)=\frac{s+a}{s}E(s)=E(s)+a\frac{E(s)}{s}\xrightarrow{\mathcal{L}^{-1}}u(t)=e(t)+a\int_{0}^{t}e(\tau)d\tau\]

El método de diseño es todavía más sencillo que el caso anterior porque sólo haya que elegir la constante de tiempo \(T\) del cero del compensador de forma que éste quede entre una década y una octava antes de la frecuencia de cruce de ganancias de la planta cuyo transitorio no se quiere modificar.

Ejemplo de diseño usando lugar de las raíces (MUY DIFÍCIL)

El avión Piper Dakota tiene una función transferencia entre la entrada ángulo del elevador y el ángulo de ataque del avión (attitude pitch)

\[ G(s) = \dfrac{\theta(s)}{\delta_e(s)} = \dfrac{160(s+2.5)(s+0.7)}{(s^2+5s+40)(s^2+0.03s+0.06)} \]

1. Diseñar un piloto automático tal que la respuesta a una entrada de referencia en el ángulo de ataque tenga un tiempo de crecimiento (rise time) menor a 1 segundo y que su sobrevalor sea menor al 10%

2. Cuando hay una perturbación constante sobre el avión tal que el piloto automático tenga que suministrar una fuerza constante sobre los controles para un vuelo estacionario, se dice que el vuela está sin ajustar (out of trim). La función transferencia entre la perturbación y el ángulo de ataque es la misma que la de la anterior, es decir:

\[G_d(s) = \dfrac{\theta(s)}{M_d(s)} = \dfrac{160(s+2.5)(s+0.7)}{(s^2+5s+40)(s^2+0.03s+0.06)}\]

donde \(M_d\) es la perturbación, que es el momento perturbativo actuante sobre el avión. Existe una superficie aerodinámica para ajustar esto, \(\delta_t\) que puede ser actuada y cambiará el momento actuante sobre el avión.

La influencia de esta perturbación \(M_d\) y \(\theta_t\) se muestra en el diagrama de la izquierda.

Para las formas de actuación manual y con piloto automático es deseable que haya un ajuste del trim para que no haya esfuerzo de control por el elevador (eso es, \(\delta_e=0\)). En vuelo manual, esto significa el que piloto no tiene que hacer fuerza sobre los mandos para mantener la altitud, mientas que para el control de piloto automático, se reduce la cantidad de potencia eléctrica requerida y el ahorro de mantenimiento y recambio de los servomotores y actuadores del elevador. Diseñar un piloto automático que comande el ajuste de trim con el uso de \(\delta_t\) tal que lleve a \(\delta_e=0\) para una perturbación constante \(M_d\) y que además cumpla con las especificaciones del punto anterior.

Solución

Para satisfacer el requerimiento de que el tiempo de crecimiento \(t_r <1\)seg indica que para un sistema de segundo orden ideal, \(\omega_n\) debe ser más grande que 1.8 rad/seg. Y para lograr un sobrevalor menor al 10% se debe tener un coeficiente de amortiguamiento \(\zeta >0.6\). En el proceso de diseño, podemos examinar el lugar de raíces para buscar un candidato compensar mediante realimentación y luego observar la respuesta de tiempo resultante cuando las raíces parecen satisfacer las pautas de diseño.

Sin embargo, dado que este es un sistema de cuarto orden, las pautas de diseño pueden no ser suficientes o pueden ser demasiado restrictivas.

Para iniciar el proceso de diseño, a menudo es útil observar las características del sistema con realimentación proporcional, es decir, el compensador \(D(s) = 1\). Los comandos para crear el lugar de raíces con respecto a \(K\) y una respuesta de tiempo para el caso de realimentación proporcional con \(K = 0.3\) son las siguientes:

s = ctrl.tf('s')
sysG = (160* (s+2.5)*(s+0.7))/((s**2+5*s+40)*(s**2+0.03*s+0.06))
_=ctrl.rlocus(sysG, grid=False) # el guión bajo es para no tener las puntos de las raíces y las ganancias como salidas por pantalla
plt.gcf().set_size_inches(8,6)

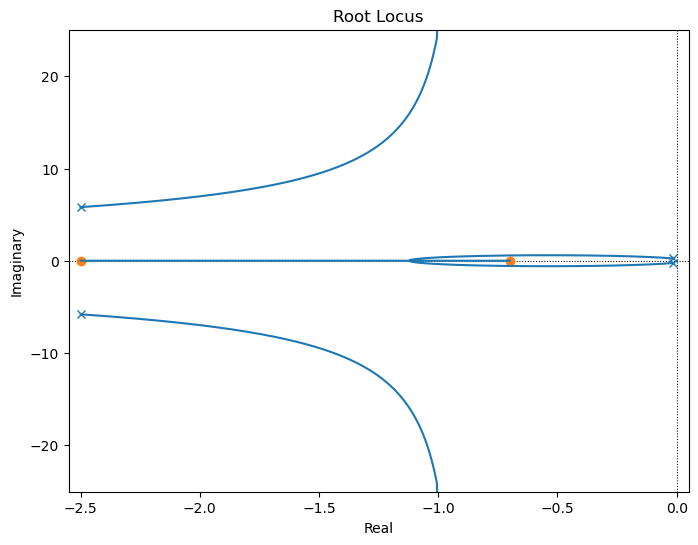
Podemos ver que para lograr el tiempo de respuesta con las dos raíces rápidas deseadas como mínimo tenemos que darle una ganancia de 0.3. Sin embargo para esta ganancia el sobrevalor va a dar más grande ya que que coeficiente de amortiguamiento es de 0.19 que es menor 0.6 requerido.

Estos polos lentos tendrán algún efecto en las respuesta y causarán un establecimiento más largo. Sin embargo, la característica dominante de la respuesta que determina si la compensación cumple o no con las especificaciones es el comportamiento en los primeros segundos, dictado por las raíces rápidas. El bajo amortiguamiento debido a las raíces rápidas hace que la respuesta temporal sea oscilatoria, lo que conduce a un sobrevalor excesivo y a un tiempo de asentamiento más prolongado de lo deseado. Esto lo podemos ver en la siguiente simulación:

K=0.3
sysT= ctrl.feedback(sysG*K, 1)

Defino una función en python para no tener que andar escribiendo siempre lo mismo o evitar el peligroso «copiar/pegar»

def graficar_respuesta_escalon(sys,T=None, title='Respuesta al escalón'): 
    t,y = ctrl.step_response(sys, T)
    fig, ax= plt.subplots(figsize=(12,4))
    ax.plot(t,y)
    ax.set_title(title)
    ax.set_xlabel("Tiempo")
    ax.grid()

Ahora si puedo utilizar la función creada recientemente

graficar_respuesta_escalon(sysT, T=np.linspace(0,8,500))

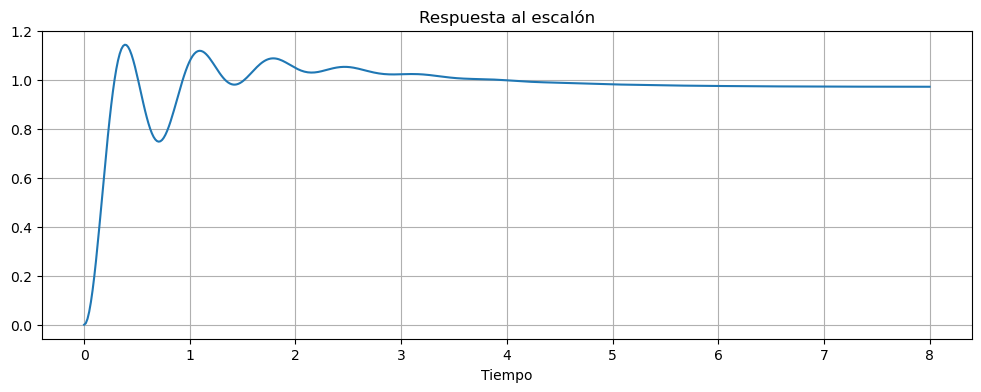
Vimos anteriormente que la compensación de lead hace que el lugar se desplace hacia la izquierda. Aquí es necesario un compensador de este para aumentar el amortiguamiento y para el \(\omega_n\) requerido. Se requerirá alguna prueba y error para llegar a la ubicación de un polo y cero adecuado. Valores de \(z = 3\) y \(p = 20\) en la ecuación tienen un efecto sustancial al mover las ramas rápidas del lugar hacia la izquierda; así resultaría: $\(D(s) = \frac{s+3}{s+20}\)$

También se requiere alguna iteración mediante prueba y error para llegar a un valor de \(K\) que cumpla con las especificaciones.

sysD = (s+3)/(s+20)
sysDG=sysG*sysD
_=ctrl.rlocus(sysDG, grid=False)
plt.gcf().set_size_inches(8,6)

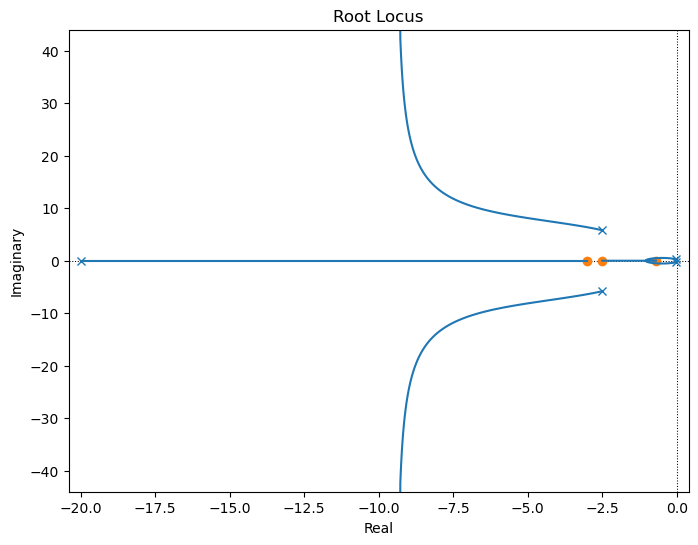
Entonces probamos con esta ganancia de \(K=1.5\)

K=1.5
sysKDG=sysDG*K
sysT = ctrl.feedback(sysKDG,1)
graficar_respuesta_escalon(sysT, T=np.linspace(0,6, 600))

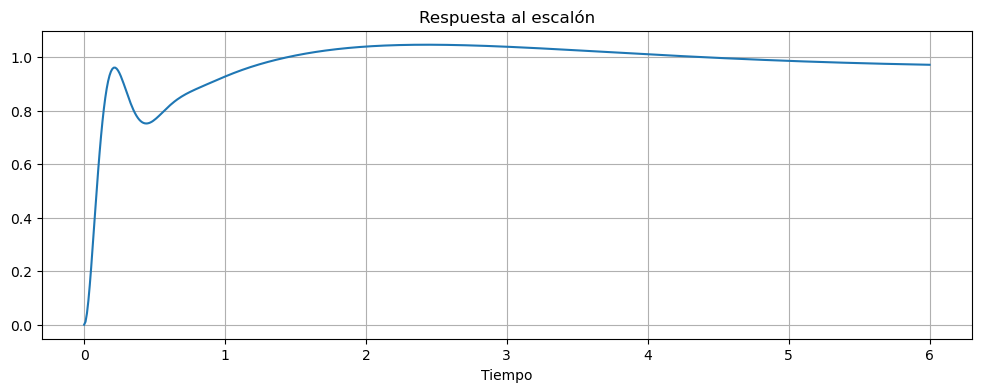
Hay que tener en cuenta que el amortiguamiento debido a las raíces rápidas que corresponde a \(K = 1.5\) es \(\zeta = 0.52\), que es ligeramente menor de lo que nos gustaría; Además, la frecuencia natural es \(\omega_n= 15\) rad/seg, mucho más rápido de lo que necesitamos. Sin embargo, estos valores son lo suficientemente cercanos como para cumplir con las pautas para sugerir un vistazo a la respuesta temporal. De hecho, la respuesta temporal que \(t_r \approx 1.1\) seg y \(M_p \approx 8\%\), que están muy cerca de cumplir especificaciones.

En resumen, la forma de diseño consistió en ajustar la compensación para influir en las raíces rápidas, examinar su efecto en la respuesta temporal y continuar la iteración de diseño hasta que se cumplieran las especificaciones.

Para estar seguro de que se cumplen las especificaciones debemos hacer:

ctrl.step_info(sysT, T=np.linspace(0,10,1000))

{'RiseTime': 0.12012012012012012,
 'SettlingTime': 5.205205205205205,
 'SettlingMin': 0.7521738729990592,
 'SettlingMax': 1.0465819498526223,
 'Overshoot': 8.64517384184365,
 'Undershoot': 0,
 'Peak': 1.0465819498526223,
 'PeakTime': 2.4324324324324325,
 'SteadyStateValue': 0.963302752293578}

Que vemos que en realidad da un poco afuera de especificaciones el tiempo de respuesta.. pero lo dejaremos así. Quizás aumentando \(K\) podamos mejorar un poco, siempre cuidando de no quedar afuera con el sobrevalor.

K=1.9
sysKDG=sysDG*K
sysT = ctrl.feedback(sysKDG,1)
ctrl.step_info(sysT)

{'RiseTime': 0.10277692351445941,
 'SettlingTime': 4.815832987534669,
 'SettlingMin': 0.7767298504310534,
 'SettlingMax': 1.03951685919739,
 'Overshoot': 7.078052413565734,
 'Undershoot': 0,
 'Peak': 1.03951685919739,
 'PeakTime': 2.305139570252875,
 'SteadyStateValue': 0.9708029197080292}

El propósito del ajuste es proporcionar un momento que elimine el valor distinto de cero en estado estacionario (después que pse mucho tiempo) del elevador \(\delta_e\). Por lo tanto, si integramos el comando del elevador \(\delta_e\) y alimentamos esta integral al dispositivo de compensación, la compensación eventualmente debería proporcionar el momento requerido para mantener una altitud arbitraria, eliminando así la necesidad de un estado estacionario \(\delta_e\).

Si la ganancia en el término integral \(K_i\) es lo suficientemente pequeña, el efecto desestabilizador de agregar la integral debería ser pequeño y el sistema debería comportarse aproximadamente como antes, ya que ese lazo de realimentación se ha dejado intacto. El diagrama de bloques se puede reducir a lo que se ve en la parte de la derecha de la figura anterior. Sin embargo, es importante tener en cuenta que, físicamente, habrá dos salidas de la compensación:\(\delta_e\) (utilizada por el servomotor del ascensor) y \(\delta_t\) (utilizado por el servomotor de compensación de trim).

Así podemos definir un nuevo controlador \(D_I\) que representará todo lo azul de la figura anterior.

\[D_I(s) = KD(s)\left(1+\frac{K_i}{s}\right)\]

La ecuación característica del sistema con el término integral será:

\[1+KDG+\dfrac{K_I}{s}KDG=0\]

Para ayudar en el proceso de diseño, es deseable encontrar el lugar geométrico de las raíces cuando se varía \(K_I\), pero la ecuación característica no se encuentra en las formas en que el lugar geométrico se pueda graficar. Por lo tanto, podemos dividir por \(1 + KDG\) y obtenemos:

\[ 1 + \dfrac{(K_I/s)KDG}{1+KDG} = 0 \]

Entonces para hacer el lugar de las raíces cuando se varía \(K_I\) debemos introducir en Python:

\[L(s) = \frac{1}{s}\frac{KDG}{1+KDG}\]

Notar que la expresión anterior es la que habíamos definido anteriormente con el nombre sysT. Haría falta multiplicarla por un integrador:

sysL=sysT*1/s
_=ctrl.rlocus(sysL)
plt.gcf().set_size_inches(8,6)

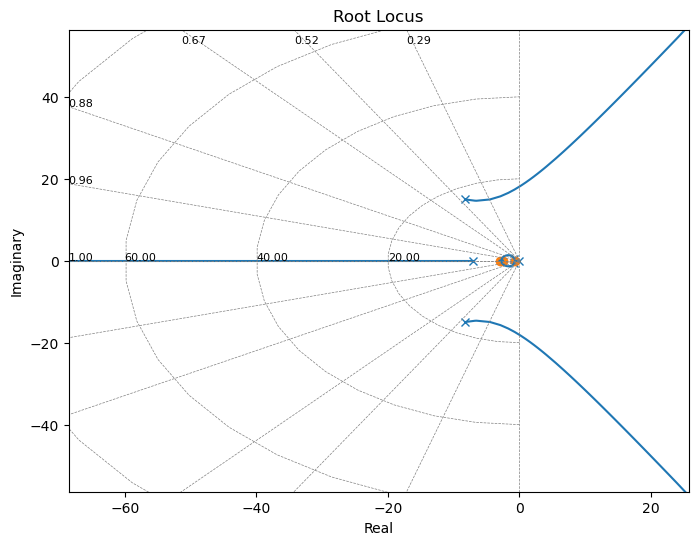
La segunda figura es la ampliación de lo que está sucediendo con los polos lentos. Podemos ver que están todos muy cerca de ceros por lo que la influencia neta que tendrán en la respuesta será muy pequeña.

Implementamos un escalón entonces para la perturbación y vemos como se comporta el lazo cerrado.

Ki=0.1
Di=K*sysD*(1+Ki/s)

Para probar tenemos que generar el sistema realimentado. Notar que para la perturbación la función de lazo quedaría:

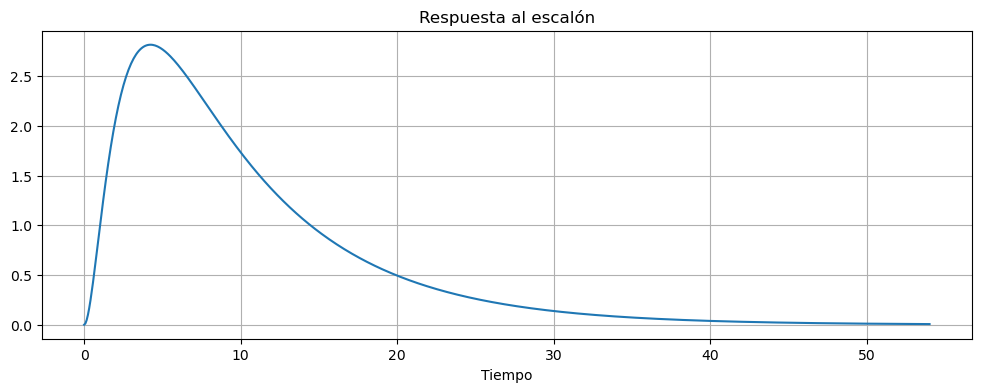
Td=ctrl.feedback(G,Di) #Ki=0.19

graficar_respuesta_escalon(Td)

T=ctrl.feedback(G*Di,1)
graficar_respuesta_escalon(T)

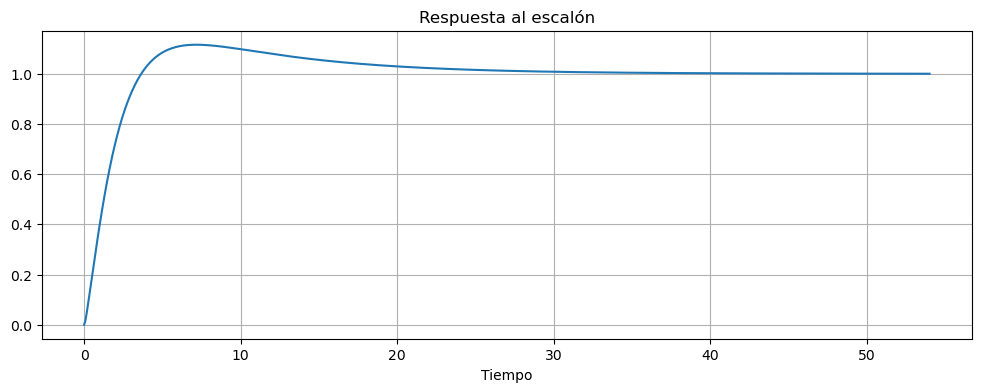
ctrl.step_info(T)

{'RiseTime': 2.595721651574587,
 'SettlingTime': 23.118145959336164,
 'SettlingMin': 0.9106676824507042,
 'SettlingMax': 1.1159845187563333,
 'Overshoot': 11.59845187563333,
 'Undershoot': 0,
 'Peak': 1.1159845187563333,
 'PeakTime': 7.138234541830114,
 'SteadyStateValue': 1.0}

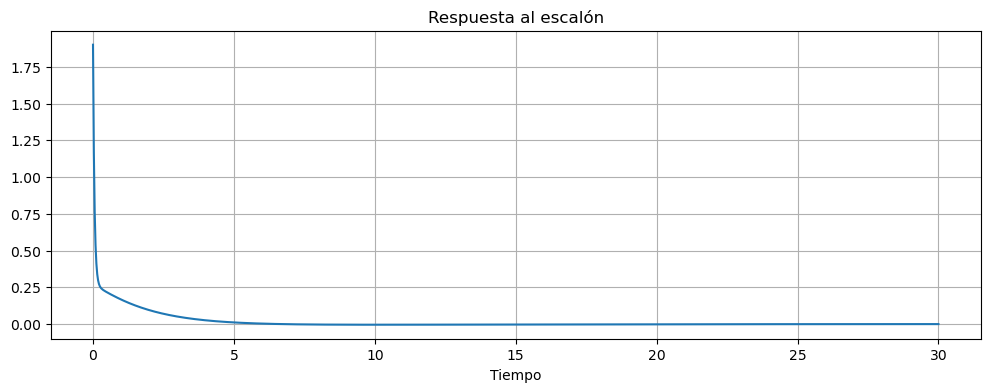
Si quisiésemos graficar como se comporta el ángulo \(\delta_e\) frente a un cambio en la referencia deberíamos pensar que esta es la salida (hacer diagrama de bloques), es decir:

T_re = ctrl.feedback(Di,G)
graficar_respuesta_escalon(T_re, T=np.linspace(0,30,1000))