Lugar de las raíces usando Python#
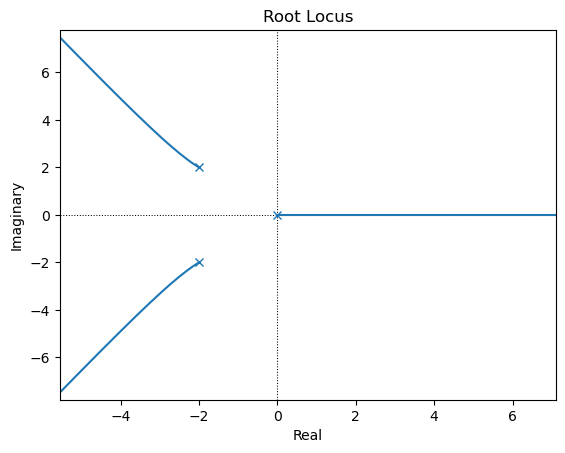
G=ctrl.tf([1,1],[1,9, 0, 0])
_=ctrl.rlocus(G, grid=False, plot=True)
El símbolo _ evita que envíe a consola lo que devuelve la función rlocus. Si queremos obtener lo que devuelve deberíamos escribir.
r=ctrl.rlocus(G, plot=False)
type(r)
tuple
Como podemos ver, r es una tupla con dos array. El primero contiene la posición de las raíces y la segunda la ganancia para las cuales se dan esas raíces.
Recordando lo que vimos en la introducción a Python podemos expandir la tupla y poner los dos datos (ganancias y raíces para cada ganancia) en dos variables separadas.
roots_list, k = r
o bien directamente podemos hacer lo mismo con
roots_list, k = ctrl.rlocus(G, plot=True, grid=False)

Condición de Magnitud y Fase para un punto en particular del plano \(s\)#
En Python para evaluar la función transferencia en un punto del plano \(s\), solo es necesario:
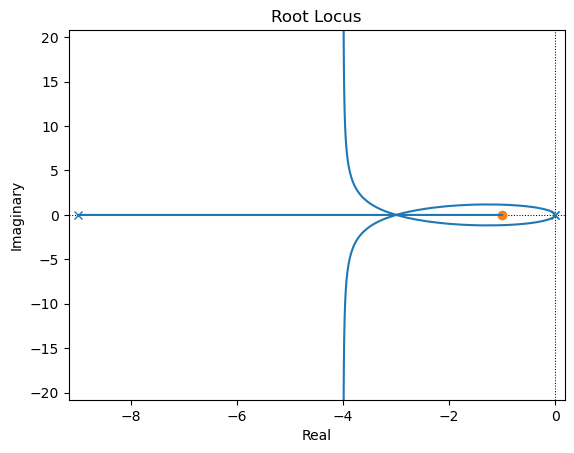
G2=ctrl.tf([1],[1, 4, 8, 0])
pto=-0.667+2j
G2(pto)
(-0.08439398595769328+1.89881723735337e-05j)
Para calcular \(K\) debemos saber que en ese punto la modulo de \(\left|KG(s)\right|\) debe ser 1. Entonces
Sabiendo que la función abs de numpy aplicada sobre un número complejo o un vector devuelve el módulo, podemos realizar la cuenta anterior en Python de la siguiente manera:
K=1/np.abs(G2(pto))
K
11.849185262917501
Para verificar que ese punto es efectivamente lugar geométrico de las raíces podemos hacer
np.angle(G2(pto))*180/np.pi
179.98710877194665
# o en grados
np.angle(G2(pto),deg=True)
179.98710877194665
Podemos ver que si bien el resultado no es 180, es un número muy cercando a este, por que el lugar de las raíces pasa por un punto muy cercano al evaluado cuando la ganancia es un número muy cercano a 11.85.
z1=G2(-.5+2.2j)
z2=G2(-.5-2.2j)
theta1=np.angle(z1,deg=True)
theta2=np.angle(z2,deg=True)
print(theta1,theta2)
179.25491462417511 -179.25491462417511
Con el cálculo anterior pretendo mostrar que la función angle() devuelve el ángulo de un número complejo, el signo depende del cuadrante donde se encuentre el número complejo. Por lo que, hay que tener cuidado a la hora de usarlo e interpretarlo.
Trazado del lugar geométrico de las raíces para ganancias negativas#
Internamente Python grafica el lugar de las raíces tomando una serie de ganancias y calculando los polos del sistema a lazo cerrado.
Para obtener el Lugar geométrico de las raíces para ganancias negativas lo único necesario será cambiar el signo a la función transferencia.
Para el ejemplo anterior, el lugar de las raíces sería:
_=ctrl.rlocus(-G2, grid=False)