Diseño del sistema de control del atitud de un satélite

Definimos el sistema:

import numpy as np
import control as ctrl
import matplotlib.pyplot as plt
%matplotlib inline

Diseñar un compensador para la planta:

\[\begin{split} \dot{\mathbf{x}}=\begin{bmatrix} 0&1\\ 0&0\\ \end{bmatrix}\mathbf{x}+\begin{bmatrix} 0\\ 1 \end{bmatrix}u\end{split}\]

\[ y=\begin{bmatrix} 1&0\end{bmatrix}\mathbf{x}.\]

que ubique los polos tal que \(\omega_n =1\) y \(\zeta=0.707\):

A=[[0,1],[0,0]]
B=[[0],[1]]
C=[[1,0]]
D=[[0]]
sys=ctrl.ss(A,B,C,D)

Análisis de Controlalibidad y Observabilidad

Vemos que el sistema es controlable usando las matrices C y B dadas. Aunque no lo sería se fuesen diferentes (es decir se actuara o se midiera diferente).

print(np.linalg.matrix_rank(ctrl.obsv(A,C)))

print(np.linalg.matrix_rank(ctrl.obsv(A,[[0,1]])))

print(np.linalg.matrix_rank(ctrl.ctrb(A,B)))

print(np.linalg.matrix_rank(ctrl.ctrb(A,[[1],[0]])))

2
1
2
1

Para cumplir con los requerimientos debemos ubicar los polos en \(\alpha_c = -0.7070 \pm 0.0707j\).

Ley de Control

Usando el comando acker o place obtenemos la ley de control que ubica los polos del sistema donde queremos.

wnc=1
zetac=np.sqrt(2)/2
polyc=[1,2*zetac*wnc,wnc**2]
alpha_c =np.roots(polyc)
print(alpha_c)

[-0.70710678+0.70710678j -0.70710678-0.70710678j]

K = ctrl.place(A,B,alpha_c)
print(K)

[[1.         1.41421356]]

Usando acker

K = ctrl.acker(A,B,alpha_c)
print(K)

[[1.         1.41421356]]

Controlamos que las cuentas esten bien hechas, viendo que los autovalores de \(\mathbf{A}-\mathbf{BK}\) den donde tienen que dar:

l,_=np.linalg.eig(A-B@K)
print(l)

[-0.70710678+0.70710678j -0.70710678-0.70710678j]

Diseño del estimador

Ahora ubicamos los polos del estimador 5 veces más rápido, pero con un \(\zeta\) que haga que no oscile (\(\zeta=0.5\)).

wne=5
zetae=0.5
polye =[1,2*zetae*wne,wne**2]
rootse=np.roots(polye)
print(rootse)

[-2.5+4.33012702j -2.5-4.33012702j]

Lt=ctrl.place(sys.A.T,sys.C.T,rootse).T
print(Lt)

[[ 5.]
 [25.]]

Definición del sistema de control

Expresando las ecuaciones de estado del controlador \(D_c\) nos queda:

\[\begin{split}\begin{eqnarray} \mathbf{\dot{\hat{x}}}&=&(\mathbf{A-BK-LC}) \mathbf{\hat {x}}+\mathbf{L}y\\ u&=&-\mathbf{K}\mathbf{\hat{x}}\end{eqnarray}\end{split}\]

Dc=ctrl.ss(A-B@K-Lt@C,Lt,-K,[0])
ctrl.tf(Dc)

\[\frac{-40.36 s - 25}{s^2 + 6.414 s + 33.07}\]

Con este controlador podemos hacer un análisis de sistema igual que lo hacíamos con control clásico.

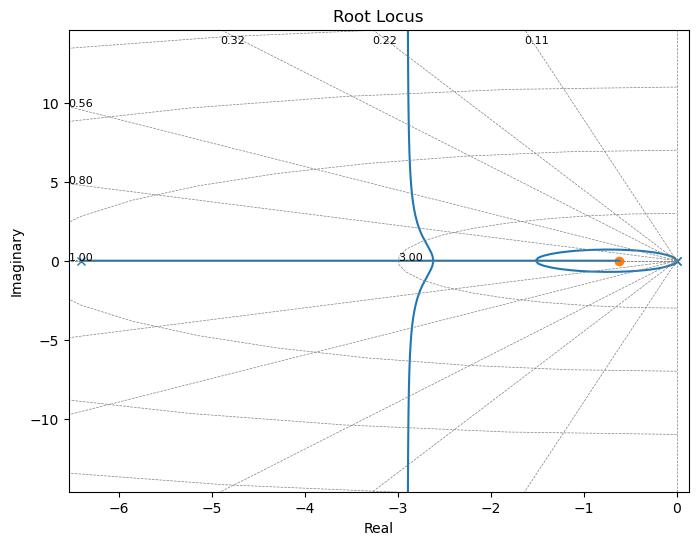
_=ctrl.bode(sys*-Dc,dB=True)
plt.gcf().set_size_inches(12,8)

ctrl.margin(sys*-Dc)

(4.624852080148206, 49.92496178414217, 5.394208336492238, 1.3670031280375023)

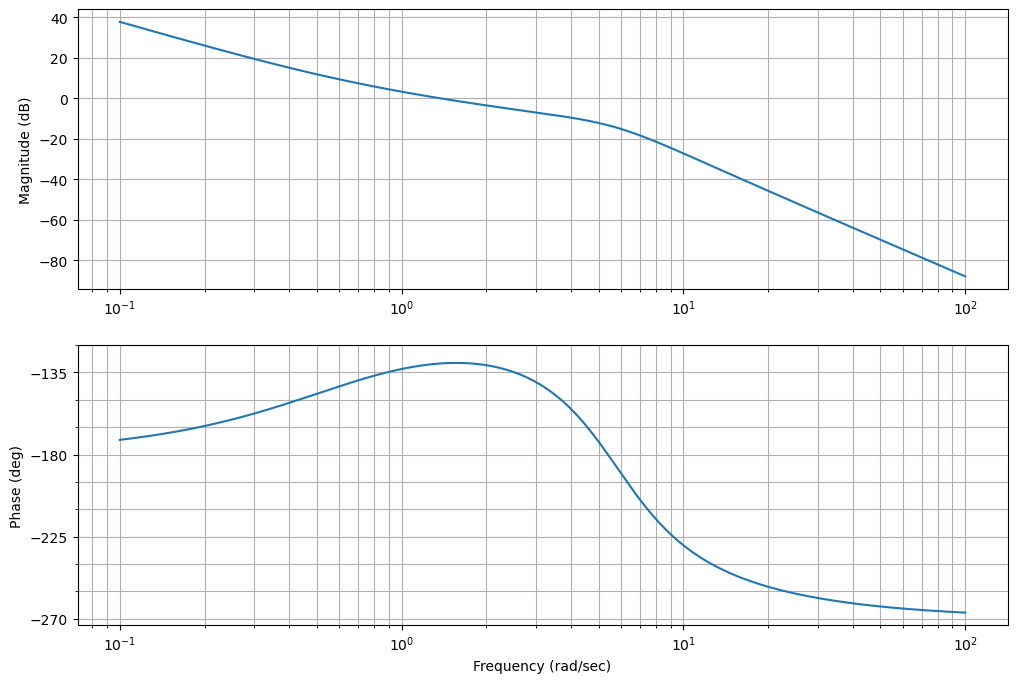
_=ctrl.rlocus(sys*-Dc,grid=True)
plt.gcf().set_size_inches(8,6)

Podemos ver que este diseño tiene un margen de fase de 50 grados aproximadamente.

Con estimador reducido

Pondremos ahora el polo del estimador en -5rad/seg.

polesered=[-5]
Aaa=sys.A[0:1,0:1]
Aab=sys.A[0:1,1:]
Aba=sys.A[1:,0:1]
Abb=sys.A[1:,1:]

Ba = sys.B[0:1,0]
Bb = sys.B[1:,0]

Ltred = ctrl.acker(Abb.T,Aab.T,polesered).T
Ltred

array([[5.]])

Ahora podemos obtener la ley de control igualmente mediante estas ecuaciones del controlador para un sistema con un estimador reducido.

Para esto necesitamos devidir las \(\mathbf K\) que multiplican a la parte medida de los esatados (\(\mathbf{K_a}\)) de la no medida (\(\mathbf{K_b}\)).

Definición del sistema controlador con estimador de orden reducido

Ka=K[0,0:1]
Kb=K[0,1:]

Ar = Abb-Ltred@Aab-(Bb-Ltred@Ba)*Kb
Br = Ar@Ltred + Aba - Ltred@Aaa - (Bb-Ltred@Ba)@Ka
Cr = -Kb
Dr = -Ka-Kb@Ltred

Dcr = ctrl.ss(Ar,Br,Cr,Dr)

ctrl.tf(-Dcr)

\[\frac{8.071 s + 5}{s + 6.414}\]

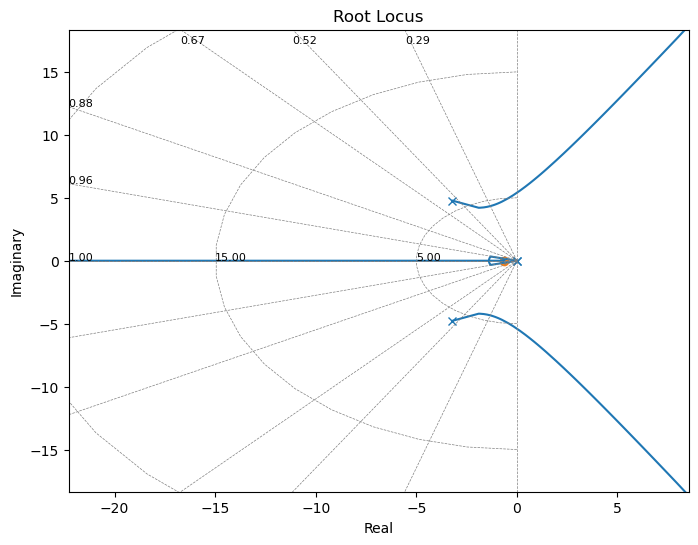
_=ctrl.bode((-Dcr*sys),dB=True)
plt.gcf().set_size_inches(12,8)

ctrl.margin(-Dcr*sys)

(9.769962616701384e-16, 53.494190654187605, 0.0, 1.3539367069138148)

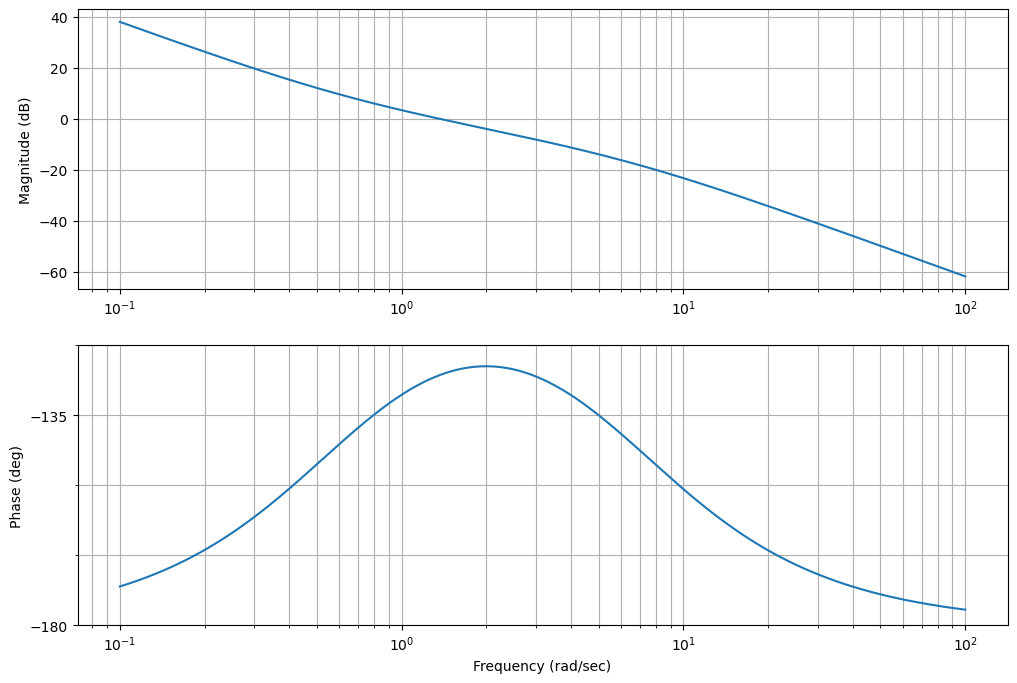
_=ctrl.rlocus(-Dcr*sys)
plt.gcf().set_size_inches(8,6)