Ecuaciones útiles para el diseño del Lead por análisis en frecuencia#
Lead#
Cero del compensador:#
Polo del compensador#
Relación entre el polo y el cero necesaria#
o misma relación escrita al reves
Frecuencia de máxima fase del compensador#
Ubicación del polo y del cero en función del \(\omega_{max}\)#
Procedimiento de Diseño:#
Obtener \(K\) para
lograr el error requerido, o para
logar el ancho de bando requerido
Evaluar el margen de fase para el sistema con el \(K\) anterior
Determinar la fase que es necesario agregar y agregarle hasta 10 grados más
Determinar el valor de \(\alpha\)
Elegir el \(\omega_{max}\) que deseamos como la frecuencia de corte y ubicar el cero \(z=-\omega_{max}\sqrt{\alpha}\) y el polo \(p=\dfrac{-\omega_{max}}{\sqrt{\alpha}}\) 6.Dibujar la respuesta el frecuencia del sistema con el compensador. Evaluar si se cumplen con los requerimientos.
Iterar sobre este diseño variando la posición del polo, del cero y de la ganancia. En caso de ser necesario usar dos compensadores.
Ecuaciones útiles para el diseño del Lag por análisis en frecuencia#
Lag#
Cero del compensador:#
Polo del compensador#
La ganancia agregada será#
Procedimiento de diseño de un Lag#
Determinar la ganancia \(K\) que permite cumplir con los requerimientos de margen de fase
Dibujar el Diagrama de bode del sistema sin compensar pero con el \(K\) obtenido
Determinar el \(\alpha\) que permita cumplir con las especificaciones de baja frecuencia (error en estado estacionario)
Elegir la posición del cero del compensador que su frecuencia \(\omega = \dfrac{1}{T_I}\) encuentre entre una octava y una decada más abajo que la nueva frecuencia de cruce \(\omega_c\)
La otra frecuencia será entonces \(\omega=\dfrac{1}{\alpha T_I}\)
Iterar en el diseño. Ajustar parámestros (polo, cero y ganancia) para cumplir todas las especificaciones.
Ejemplo de diseño con un Lead#
La siguiente planta representa un sistema térmico:
Con un compensador Lead logar los siguientes requerimientos:
Error de estado estacionario menor a 0.1 frente a una entrada escalón unitario
Margen de fase 40 grados
Vamos a averiguar que sobrevalor esperamos para ese margen de fase
zeta=40/100
sv=np.exp(-np.pi*zeta/np.sqrt(1-zeta**2))
sv
0.2538267219801087
Ahora definimos nuestro sistema
s=ctrl.tf('s')
G=1/((s/0.5+1)*(s+1)*(s/2+1))
G
Y analizamos la ubicación de los polos a lazo abierto.
G.pole()
array([-2. +0.j, -1. +0.j, -0.5+0.j])
Vamos a analizar además la ganancia en estado estacionario.
ctrl.dcgain(G)
1.0
Esto es lo mismo que evaluar el módulo de la función \(|G(s)|\) en \(s=0\). Verificamos:
np.abs(G(0))
1.0
Definimos en \(K\) la ganancia necesaria que debe tener nuestro sistema para que el error sea 0.1. Recordando que para un sistema de tipo 0
Se tiene que:
\(K\) debe ser igual a 9 para que el error sea 0.1.
K=9
Como nuestro sistema tiene y auna ganacia de 1, aplicandole el valor de \(K\) obtendremos el error de estado estacinario requerido para el sistema.
Vamos a analizar ahora que pasa con nuestro diagrama de Bode y los margenes de fase de estabilidad con esa ganancia.
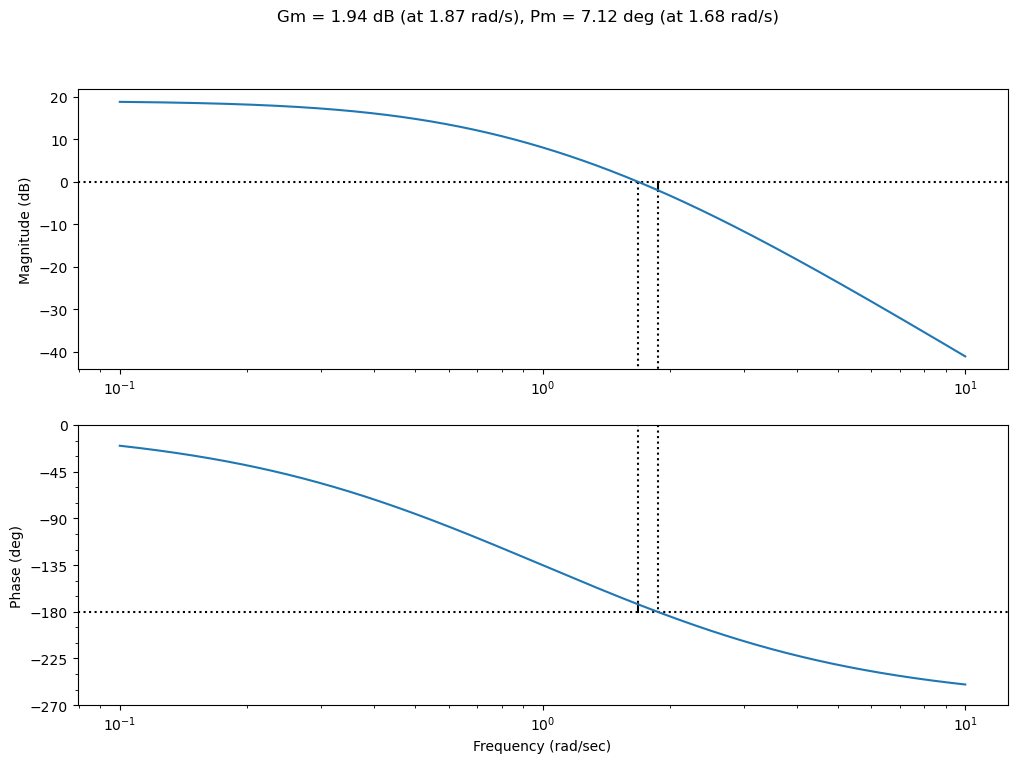
ctrl.bode_plot(K*G, dB=True, margins=True);
plt.gcf().set_size_inches(12,8)
_, pm, _, _,wp,_ = ctrl.stability_margins(K*G)
pm, wp
(7.124875100212705, 1.6844247549145053)
Vemos que tenemos 7 grados de margen de fase y en una frecuencia aproximada de 1.7 rad/seg. Sieguiendo las recomendaciones escritas anteriormente podemos definie el ángulo que queremos agregar. Debido a que tenemos 7 grados, necesitamos 40 gados en total y se recomienda dejarse 10 grados para ajustar, nos queda un \(\phi_{max} = 40 - 7 + 10 =43\)
phi_max=43
Vamos a pasar esto a rad
phi_max=phi_max*np.pi/180
phi_max
0.7504915783575616
Para lograr este ángulo máximo con un compensador de adelanto, se encesita un \(\alpha\) de
alpha = (1-np.sin(phi_max))/(1+np.sin(phi_max))
alpha
0.1890618014191675
Vamos a comenzar ubicando el máximo en el punto de donde cruza los 0 db el bode antes de poner el compensador.
wmax=wp
wmax
1.6844247549145053
Ahora obtenemos el parámetro \(T_D\) del lead:
TD=1/(wmax*np.sqrt(alpha))
Por útimo obtenemos las posiciones del polo y del cero
z=-1/TD
p=-1/(alpha*TD)
print(z, p)
-0.7324087281273646 -3.873911718970384
Dc=K*ctrl.tf([-1/z, 1],[-1/p, 1])
Dc
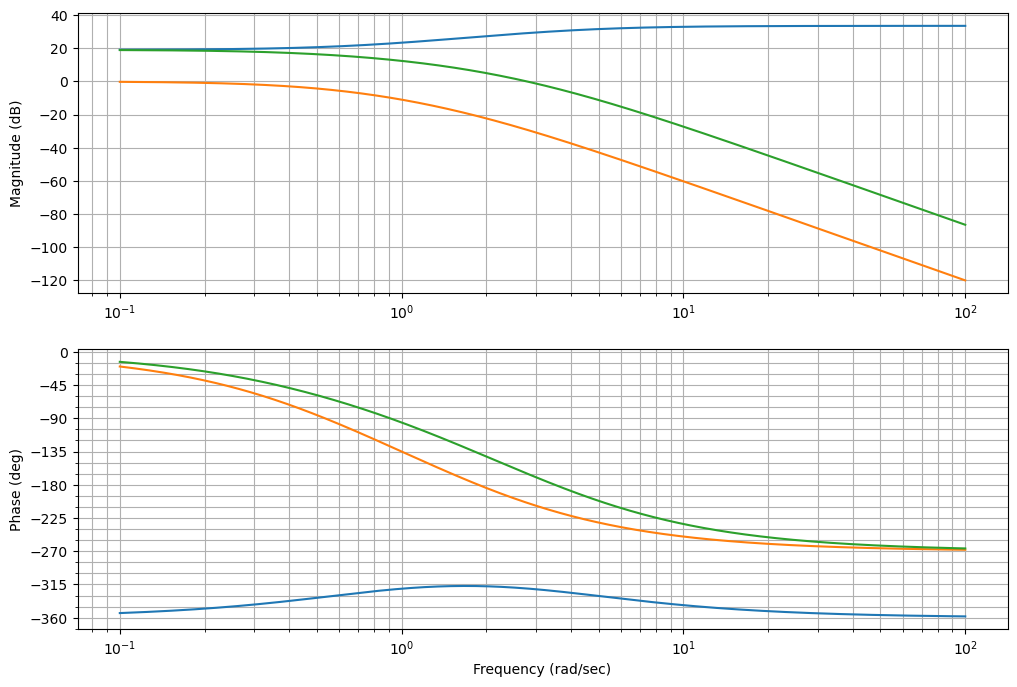
ctrl.bode([Dc,G, Dc*G], dB=True);
plt.gcf().set_size_inches(12,8)
ctrl.stability_margins(Dc*G)
(1.5861221359594695,
15.136384753425546,
0.21189015906308178,
3.4948275411263174,
2.7862036560201884,
2.982644855304859)
Podemos ver que el diseño no resultó como queriamos. Esto es debido a que como pusimos un lead con ganacia estacionaria igual a 1, nos agegó ganancia mayores a 1 en la zona de corte de 0 db, produciendo un aumento de la frecuencia en la que corta y una disminución de fase debido a que ahora este margen de fase se mide sobre una frecuencia mayor.
T=ctrl.feedback(Dc*G)
t,y = ctrl.step_response(T, np.linspace(0,20,1200))
fig, ax = plt.subplots(figsize=(12, 4))
ax.plot(t,y)
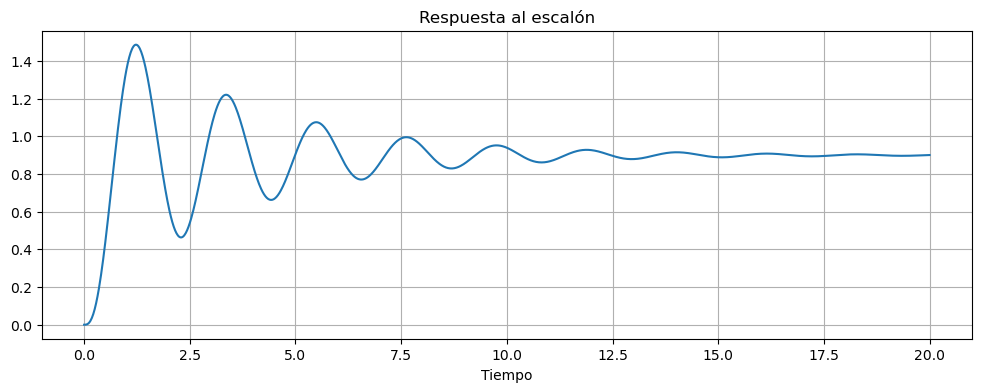
ax.set_title('Respuesta al escalón')
ax.set_xlabel('Tiempo')
ax.grid()
Show code cell source
ctrl.step_info(T)
{'RiseTime': 0.43174879695363766,
'SettlingTime': 13.1569764966398,
'SettlingMin': 0.46341576424197717,
'SettlingMax': 1.4864876051310991,
'Overshoot': 65.165289459011,
'Undershoot': 0,
'Peak': 1.4864876051310991,
'PeakTime': 1.2270755281840229,
'SteadyStateValue': 0.9}
Rediseño#
El problema está en que la frecuencia de corte se me corrión a la izquierda y los 10 gados que agregué no alcanzan para compensar la caida de fase de los tres polos de la planta.
Lo que voy a intentar es agregar mucha más fase y tratar de correr el cero para frecuencias más altas para que no moleste tanto su aumento módulo a en la frecuencia de corte.
Vamos a reescrbir todas las ecuacioes anteriores para que sea más facil de iterar y probar con diferentes valroes de \(\phi_{max}\) y \(\omega_{max}\).
phi_max=61*(np.pi)/180
alpha = (1-np.sin(phi_max))/(1+np.sin(phi_max))
wmax=5.1
TD=1/(wmax*np.sqrt(alpha))
z=-1/TD
p=z/alpha
Dc=K*ctrl.tf([-1/z,1],[-1/p,1])
print(Dc.zero(), Dc.pole(), Dc.dcgain(), alpha)
[-1.31894968+0.j] [-19.72023678+0.j] 9.0 0.06688305493807606
_,pm,_,_,wp,_=ctrl.stability_margins(Dc*G)
print(pm,wp)
40.32064090829249 2.2982369417072577
T=ctrl.feedback(Dc*G)
t,y = ctrl.step_response(T, np.linspace(0,20,1200))
fig, ax = plt.subplots(figsize=(12, 4))
ax.plot(t,y)
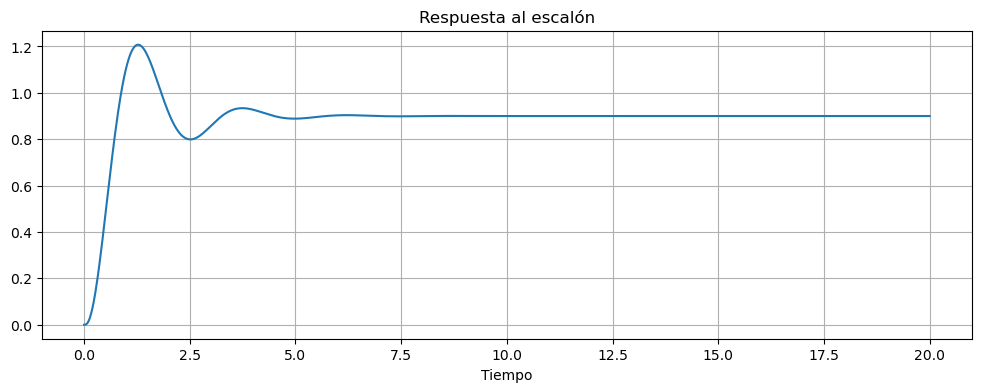
ax.set_title('Respuesta al escalón')
ax.set_xlabel('Tiempo')
ax.grid()
ctrl.step_info(T)
{'RiseTime': 0.5086798070739117,
'SettlingTime': 4.172549228295465,
'SettlingMin': 0.7992969205341778,
'SettlingMax': 1.2076146102903595,
'Overshoot': 34.17940114337328,
'Undershoot': 0,
'Peak': 1.2076146102903595,
'PeakTime': 1.2785735691317242,
'SteadyStateValue': 0.9}
ctrl.rlocus(Dc*G);
fig=plt.gcf()
fig.set_size_inches(8,6)
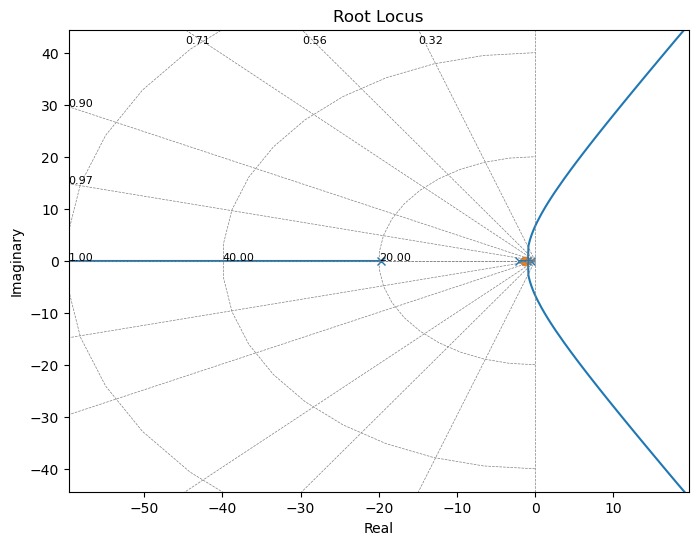
Problema#
La sisguiente planta representa un sistema térmico: $\(\frac{1}{(\frac{s}{0.5}+1)(s+1)(\frac{s}{2}+1)}\)$ Con un compensador Lag logar los siguientes requerimientos:
Error de estado estacionario menor a 0.1 frente a una entrada escalón unitario
Margen de fase 40 grados
Vamos a resolver el mismo problema que resolvimos anteriormente, pero ahora con un Lag.
plt.figure()
ctrl.bode(G, margins=True);
plt.gcf().set_size_inches(12,8)
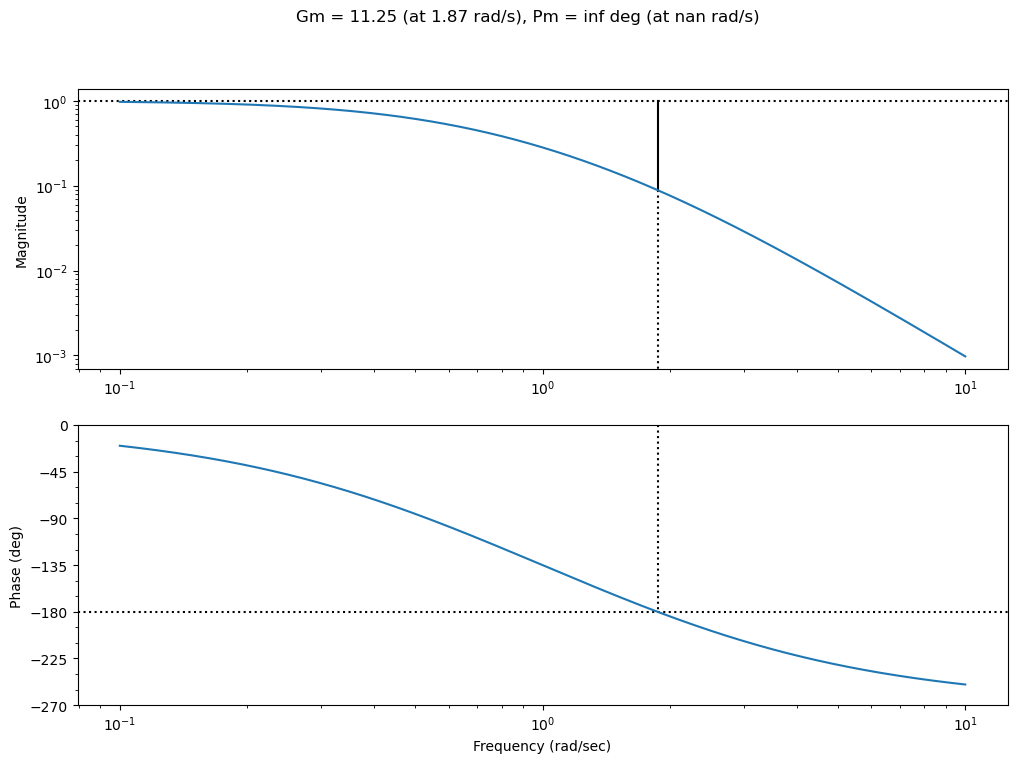
Con el controlador Lag no podemos mejorar el margen de fase, ya que quita fase para toda \(\omega\). Para lograr el margen de fase requerido vamos a darle una ganacia al sistema tal que la frecuencia de cruce por 0dB sea la necesria para que el margen de vase de lo necesario para cumplir con este requerimeinto.
Ya que nos piden un margen de fase de 40 grados, lo que vamos a hacer es ver a que frencuencua se tiene -140 de fase y vamos a ver que gancia es necesaria agregarle a la planta para que cruce por 0dB a esta frecuencia, esto es:
w1=1.j
K=1/np.abs(G(w1))
K
3.535533905932737
Verificamos calculando los margenes de estabilidad
ctrl.stability_margins(K*G)
(3.1819805153394634,
45.0,
0.49933833316498616,
1.8708286933869704,
0.9999999999999999,
1.3256908836478283)
Vemos que el margen de fase es de 45 grado (algo más de lo que requerimos) y la frecuencia de cruce por 0 db es 1, comoera de eseperar.
Ahora vemos a calcular el Lag para que nos agregué la ganancia necesaria para cumplir con el error
np.abs(K*G(0))
3.535533905932737
Calculamos la relación \(\alpha\) entre el zero y el polo. Esto lo hacemos usando lo que ya sabemos que es que necesitamos una ganancia de 9 sobre la ganacia que tenemos. Esto nos dará la ganacia que necesitamos agregar
alpha = 9/ctrl.dcgain(G*K)
print(alpha)
2.545584412271572
Como criterio inicial podemos poner el cero del lag en una frecuencia 5 veces menor a la de cruce por 0 db
z=-np.abs(w1)/10
p=z/alpha
Dc2 = K*alpha*ctrl.tf([-1/z,1],[-1/p,1])
Dc2
print(Dc2.dcgain(), Dc2.pole(), Dc2.zero())
9.0 [-0.03928371+0.j] [-0.1+0.j]
plt.figure()
ctrl.bode((G, Dc2, Dc2*G), dB=True);
plt.gcf().set_size_inches(12,8)
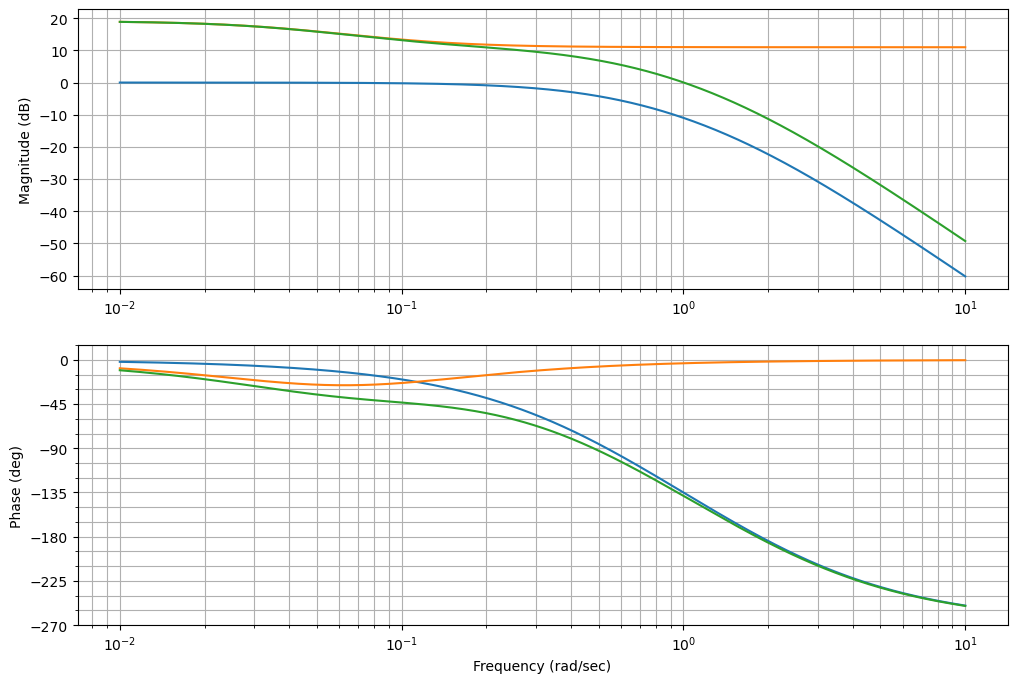
ctrl.stability_margins(Dc2*G)
(2.9878632402163476,
41.34117522250034,
0.4741712245387996,
1.8182652140041302,
1.0027882283219218,
1.2975135904967845)
T1=ctrl.feedback(Dc2*G)
t1,y1 = ctrl.step_response(T1, T=np.linspace(0,20,1200))
Show code cell source
fig, ax = plt.subplots(figsize=(12, 4))
ax.plot(t1,y1)
ax.set_title('Respuesta al escalón')
ax.set_xlabel('Tiempo')
ax.grid()
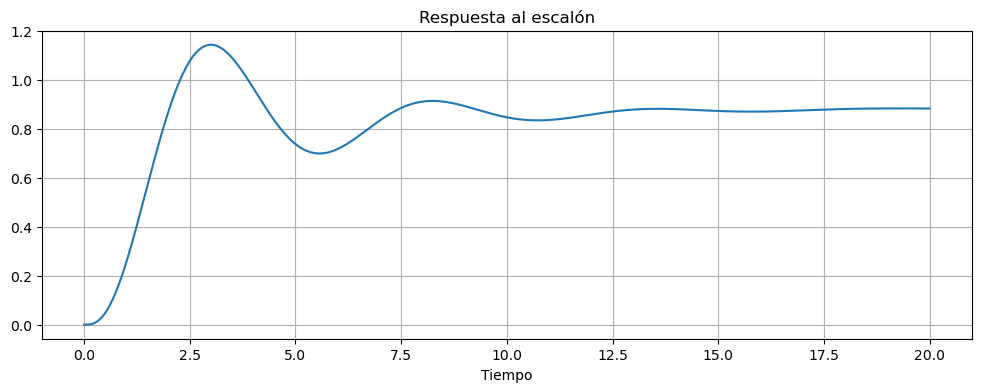
ctrl.step_info(T1)
{'RiseTime': 1.2247871296105741,
'SettlingTime': 17.979875062683227,
'SettlingMin': 0.7001740374666215,
'SettlingMax': 1.1448178821906159,
'Overshoot': 27.201986910068428,
'Undershoot': 0,
'Peak': 1.1448178821906159,
'PeakTime': 2.9884805962498007,
'SteadyStateValue': 0.9}

