Definiciones de Sistemas y Señales#
Sistema: conjunto de componentes que interactúan entre si.
Señal: es una función, típicamente del tiempo, y posiblemente de alguna otra variable (como ser coordenadas espaciales) que representa alguna magnitud de interés asociada con el sistema.
Señales#
Ejemplos de señal#
Señales de Voz (variable independiente: tiempo)#
Podemos escuchar el sonido aquí que «visualizaremos» luego en una figura aquí:
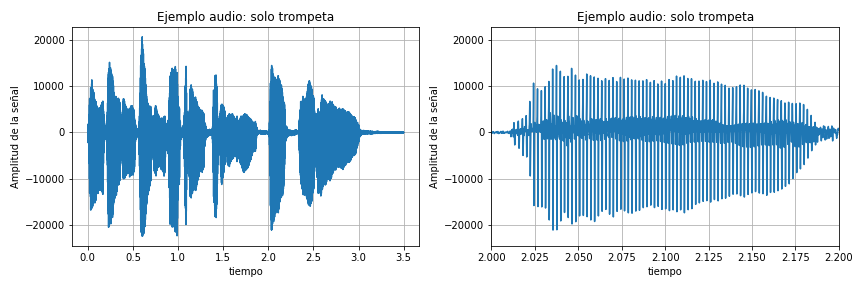
Figura 1 Señal de sonido#
Señales en un electrocardiógrafo, o electroencefalógrafo (variable independiente tiempo)#
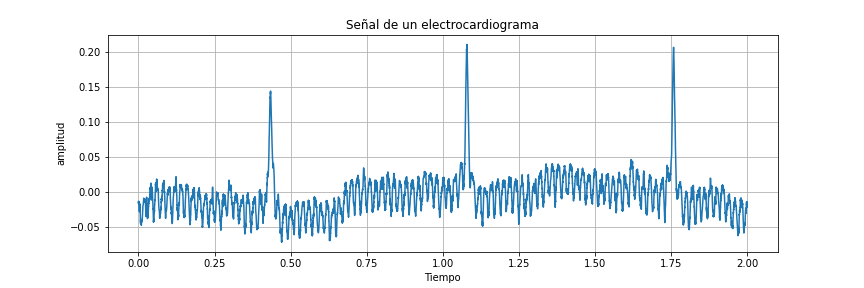
Figura 2 Señal de un electrocardiograma#
Imagen digital (dos variables independientes: coordenadas espaciales del pixel)#

Figura 3 Señal de imagen#
Definiciones relativas a las señales#
La interacción de los componentes en el sistema genera señales observables y no observables. Las observables son las que efectivamente se miden.
Las señales observables que son de nuestro interés son usualmente denominadas salidas del sistema y las denotaremos con \(y\).
El sistema está también afectado por estímulos externos. Las señales externas que pueden ser manipuladas son usualmente llamadas entradas, que denotamos con \(u\)
Las señales externas que no pueden ser manipuladas son llamadas perturbaciones que denotaremos en general con \(d\).
Las perturbaciones suelen dividirse en aquellas que pueden medirse directamente y aquellas que se ponen en evidencia sólo a traves de su influencia en las salidas.
Señales importantes#
Impulso unitario#
Esta señal impulso \(\rho(t)\) es de la siguiente forma:
Amplitud \(\dfrac{1}{T}\) en \(t=0\).
Duración \(T\).
\(T\rightarrow 0.\)
Es decir es una señal que tiene un area bajo su curva (integral) igual 1, tiene un duración que tiende a 0, y una amplitud que tiende a infinito.
Físicamente esta señal es irrealizable. Sin embargo modela bien la física en algunos eventos cotidianos, como puede ser la fuerza aplicada un cuerpo cuando se le da un martillazo, el chispazo ocurrido cuando se desenchufa un artefacto eléctrico (modela la tensión), etc.
Señal escalón#
La señal escalón se define de la siguiente manera:
Relación entre el escalón y el impulso unitario#
La relación entre el impulso y el escalón es la siguiente:
Es decir, la derivada de la función escalón es la función impulso unitario.
Sistemas#
Esquema básico de un sistema#
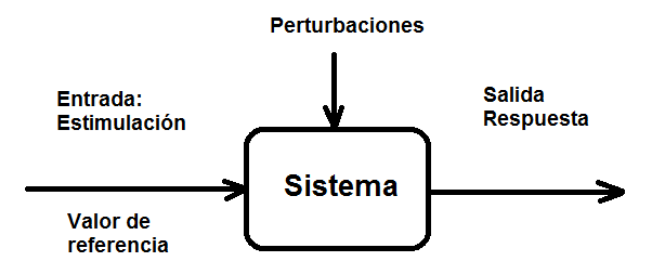
Figura 4 Sistema General#
Los sistemas no necesariamente están restringidos a sistemas físicos. Pueden ser biológicos, económicos, computacionales, informáticos, sociales, etc.
Ejemplos de sistema#
Sistema de Calefacción Sistema de Calefacción Solar Solar#
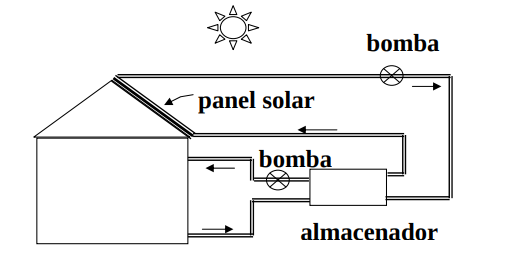
Figura 5 Sistema de calefacción solar#
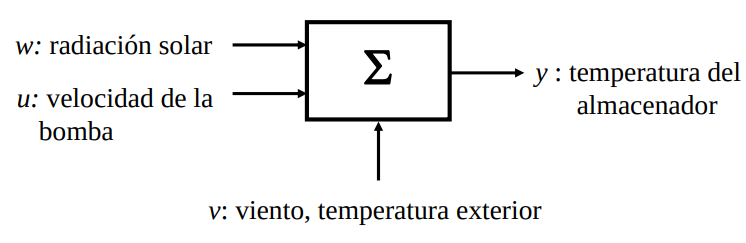
Figura 6 Esquema de sistema de calefacción solar#
Ecosistema#
Ambiente aislado compuesto por dos clases de individuos: presas (P: población de presas) y depredadores (D: población de depredadores).
Hipótesis del modelo:
En ausencia de depredadores (D=0), la población de presas crece exponencialmente.
Los depredadores sólo se alimentan de presas, por lo que en ausencia de presas (P=0), la población de depredadores se extingue exponencialmente.
Un posible modelo que verifica estas hipótesis es el de Lotka-Volterra
Propiedades de los sistemas#
Linealidad#
Un sistema es lineal si verifica el Principio de Superposición, tanto para entradas como para condiciones iniciales.
Si para una entrada \(u_1\) aplicada en el instante \(t_0\), con el sistema en un estado inicial \(\sum_0\), la salida es \(y_1\) , y para una entrada \(u_2\) aplicada en el instante \(t_0\), con el sistema en un estado inicial \(\sum_0\), la salida es \(y_2\) entonces si se aplica una \(c_1u_1 +c_2u_2\) entrada en el instante \(t_0\), con el sistema en un estado inicial \(\sum_0\), la salida será \(c_1y_1 +c_2y_2\)
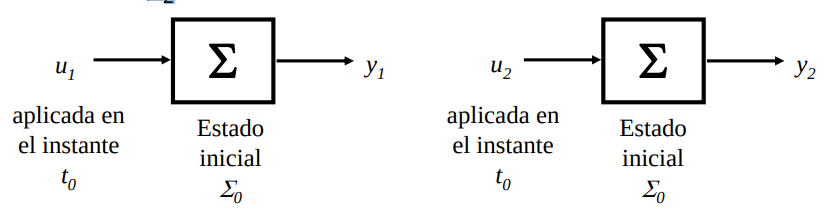
Figura 7 Hipótesis linealidad#
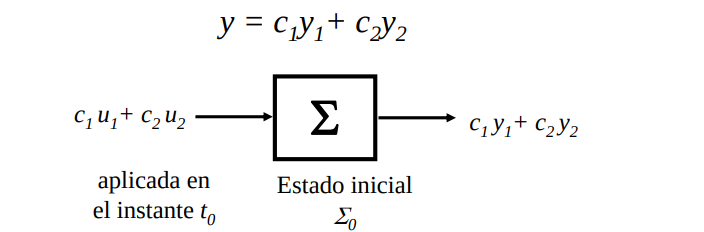
Figura 8 Requerimiento de linealidad#
Es claro que esta propiedad, como fue definida, es imposible de verificar en la práctica, ya que no se pueden realizar los ensayos propuestos en el mismo período de tiempo.
Debemos asumir entonces que el sistema no cambia con el tiempo (propiedad de estacionariedad o invariancia en el tiempo, que definiremos a continuación), de manera que podemos realizar los ensayos a distintos tiempos a partir del sistema en el mismo estado inicial.
Un sistema que no verifica el principio de Superposición se denomina no lineal.
Invariancia en el tiempo#
Un sistema es invariante en el tiempo si su salida es siempre la misma cada vez que se aplique la misma entrada (para las mismas condiciones iniciales), sin importar el instante en que se aplique la entrada. Para dar una definición más precisa, es necesario definir el operador desplazamiento temporal que notaremos: \(z_{\Delta}\) que aplicado a una función del tiempo, la desplaza temporalmente un intervalo \(\Delta\), es decir:
Desplazamiento temporal#
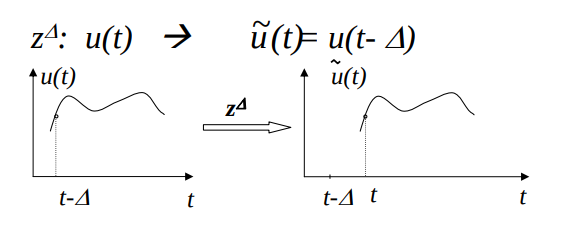
Figura 9 Operador desplazamiento temporal#
Por lo tanto, el sistema es estacionario estacionario si para una entrada \(u(t)\) aplicada en el instante \(t_0\) resulta la salida es \(y(t),\) entonces para una entrada = \(z^\Delta u(t)\) aplicada en \(t_0+\Delta\) la salida es \(\tilde y(t) =z^\Delta y(t)\)
Principio de estacionariedad o invariancia en el tiempo#
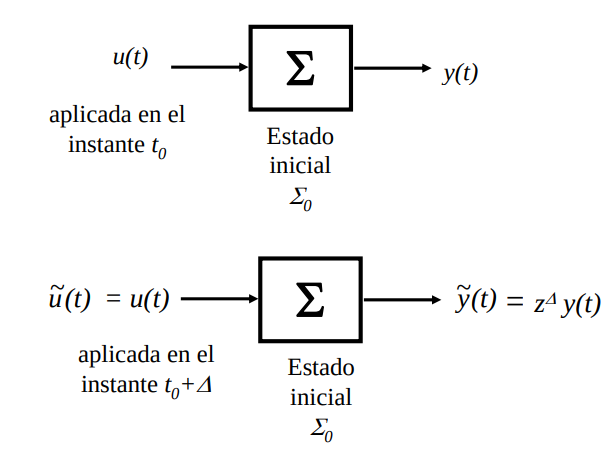
Figura 10 Invariancia en el tiempo#
Sistemas SISO (Single-Input/Single-Output)#
Un sistema con una única entrada y una única salida se denominan SISO
Sistemas MIMO (Multiple-Input/Multiple-Output)#
Sistemas con múltiples entradas y múltiples salidas se denominan MIMO
Existen ademas las variedades SIMO y MISO, que dejamos al lector que intuya a que se refieren esos nombres.
Sistemas Estáticos y Dinámicos#
Un sistema en el cual la salida en el instante \(t\) depende exclusivamente de la entrada en ese instante \(t\) es llamado Sistema Estático o sin memoria. En contraposición, un Sistema Dinámico es uno en el cual la salida en el instante \(t\) depende también de valores pasados y/o futuros de la entrada, además del valor en \(t\).
Los sistemas que estudiaremos en esta materia son los sistemas dinámicos, es decir que el valor de la salida actual depende no solo de las entradas actuales sino también de los valores de la entradas pasadas. Aunque diseñaremos también algunos controladores que pueden considerarse estáticos, es decir que cuya salida solo depende de valores presentes de la entrada del controlador
Sistemas Causales y No causales#
Un sistema es causal si su respuesta a una entrada no depende de valores futuros de esa entrada y/o valores futuros de salidas. Un sistema que no verifica esta propiedad es llamado no causal. En particular un sistema se dice anticausal si su respuesta a una entrada depende exclusivamente de valores futuros de esa entrada y/o valores futuros de salidas.
Todos los sistemas físicos son causales.
Caracterización de tipos de sistemas#
Desde el punto de vista de las ecuaciones matemáticas los sistemas se puedes clasificar como:
Tipo de Sistema |
Ecuaciones del Modelo |
|---|---|
Lineal |
Ecs. Lineales |
No Lineal |
Ecs. no Lineales |
Invariante en el tiempo |
Ecs. a coeficientes constantes |
Variante en el tiempo |
Ecs. a coeficientes en función del tiempo |
Parámetros concentrados |
Ecs. dif. Ordinarias |
Parámetros distribuidos |
Ecs. dif. Parciales |
de tiempo continuo |
Ecs. diferenciales |
de tiempo discreto |
Ecs. en diferencias |
SISO |
Número de Ecs. del modelo |
MIMO |
|
Determinístico |
x (variable determinística) |
Estocástico |
\(<x>\), \(\sigma\) (valor medio y desvío estándar) |
Ejemplo completo de un sistema electromecánico (motor eléctrico)#
Esquema de la idealización física del motor eléctrico#
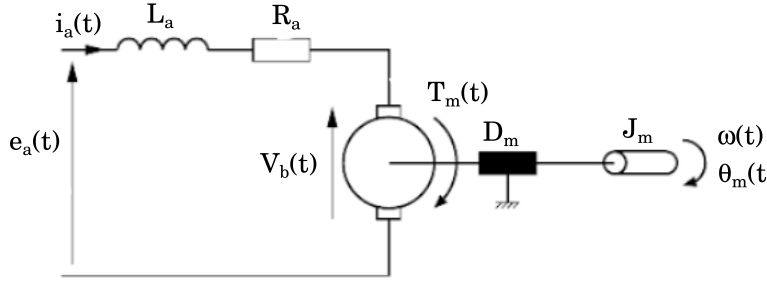
Figura 11 Diagrama idealizado del motor de corriente continua#
Diagrama del sistema desde el punto de vista de entradas y salidas#
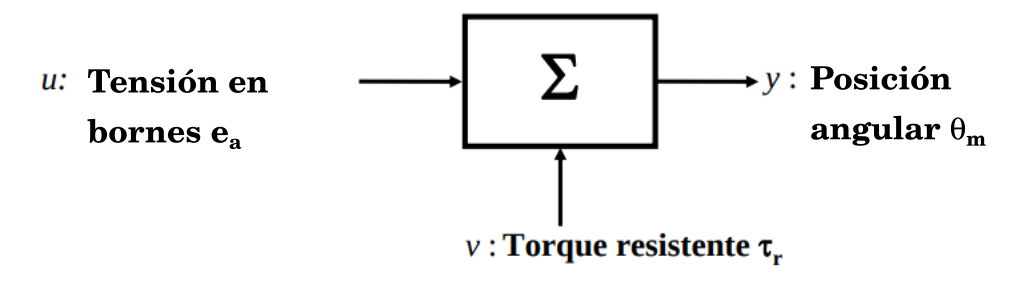
Figura 12 Esquema entrada/salida del motor de corriente continua#
Descripción del motor y su funcionamiento#
A continuación se deja un video describiendo las partes de un motor y la forma de funcionamiento.
Modelado del motor#
Los modelos matemáticos proveen de una predicción de como el sistema se va a comportar o evolucionar. En general los modelos matemáticos NO son exactos. Sin embargo, serán útiles para el diseño de los sistemas de control, debido a que este deberá proveer de la robustez requerida mediante el uso de la realimentación.
Algunas simplificaciones que consideraremos para este modelo son:
La resistencia, inductancia, masa (o momento de inercia) y «viscosidad» son constantes. Es decir, no contemplaremos cambios de ningún tipo, como por ejemplo el efecto de la temperatura.
El rozamiento viscoso es lineal. Es decir, la viscosidad es es proporcional a la velocidad (\(\tau_d=D_m*\omega\)).
Desarrollo de las ecuaciones#
El circuito eléctrico se relaciona con el mecánico, y viceversa, por medio de la siguientes ecuaciones:
para las mismas unidades \(K_t = K_b\)
Reemplazando obtenemos el sistema de ecuaciones de parámetros concentrados (no depende de la ubicación espacial de los componentes del sistema), lineal (cumple con superposición) e invariante en el tiempo (su comportamiento no cambia con el tiempo). Como el sistema es lineal e invariante en el tiempo se dice que el sistema es LTI (linear time invariant).


