Sistema masa resorte amortiguador

Ecuaciones de movimiento

Supongamos que el resorte no cumple la ley de Hook, sino que produce una fuerza que es:

\[f_k = Kx^3\]

Entonces las ecuaciones de movimiento son

\[ ma(t) = F+mg - f_b - f_k \implies m \ddot x(t) = F + mg - b \dot x(t) - K x^3(t)\]

Podemos escribir las ecuaciones de estado, suponiendo los estados son \(\dot x = x_1\) y \(x = x_2\). Entonces resultan:

\[\begin{split} \left\{ \begin{array}{ll} \dot x_1(t) = & -\dfrac{b}{m} x_1(t) - \dfrac{K} {m} x_2^3(t) +\dfrac{F(t)}{m} + g\\ \dot x_2(t) = & x_1(t) \end{array} \right. \end{split}\]

El objetivo es linealizar el sistema en torno al punto de operación. Vamos a obtener el punto de operación para \(F=0\).

Usaremos para este trabajo SymPy para que nos ayude con la matemática simbólica.

SymPy para la linealización

Primero importamos el paquete de cálculo simbólico e inicializamos la forma en que este paquete mostrará las formulas en pantalla.

import sympy as sp
sp.init_printing()

Ahora definimos los símbolos que estará presentes en las ecuaciones y luego las ecuaciones usando estos símbolos

F, m,  g, K, b, x1, x2 = sp.symbols('F, m,  g, K, b, x1, x2')
dx1 = -b/m*x1-K/m*x2**3+F/m+g
dx2 = x1

Ahora vemos como muestra SymPy las ecuaciones

dx1

ec_est=sp.Matrix([dx1,dx2])
x=sp.Matrix([x1,x2])
u = sp.Matrix([F])

Recordando un poco lo visto en teoría, podemos resolver la linealización rápidamente obteniendo el Jacobiano de las ecuaciones de estado.

A = ec_est.jacobian(x)
B = ec_est.jacobian(u)

Veamos el resultado:

A

\[\begin{split}\displaystyle \left[\begin{matrix}- \frac{b}{m} & - \frac{3 K x_{2}^{2}}{m}\\1 & 0\end{matrix}\right]\end{split}\]

B

\[\begin{split}\displaystyle \left[\begin{matrix}\frac{1}{m}\\0\end{matrix}\right]\end{split}\]

El punto de equilibrio de un sistema es donde el sistema está quieto o permanece si variar nada. Para obtener el punto de equilibrio, por lo tanto tenemos que hacer que las variables de estados \(x_1\) y\( x_2\) permanezcan constantes. Esto ocurre cuando todas las derivadas \(\dot x_1\) y \(\dot x_2\) son igual a 0 (el sistema esta quieto). Vamos a considerar en un primer momento \(F=0\).

ec_est_f0 = ec_est.subs([(F,0)]) # substituímos F con 0
sol0 = sp.solve(ec_est_f0,(x1,x2), dict=True) # resolvemos X1, y x2
sol0

Me quedo solo con la solución real, por ser la única con sentido físico

sol0 = sol0[0]
sol0

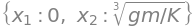
A.subs(sol0)
B.subs(sol0)

\[\begin{split}\displaystyle \left[\begin{matrix}\frac{1}{m}\\0\end{matrix}\right]\end{split}\]

Podemos resolver también ahora si ponemos una \(F=1\)

ec_est_f1 = ec_est.subs([(F,1)]) 
sol1 = sp.solve(ec_est_f1,(x1,x2),dict=True)
sol1

Me quedo con la única solución real posible que es la primera (recodar que python indexa de 0).

sol1 = sol1[0]
A.subs(sol1), B.subs(sol1) 

\[\begin{split}\displaystyle \left( \left[\begin{matrix}- \frac{b}{m} & - \frac{3 K \left(\frac{g m}{K} + \frac{1}{K}\right)^{\frac{2}{3}}}{m}\\1 & 0\end{matrix}\right], \ \left[\begin{matrix}\frac{1}{m}\\0\end{matrix}\right]\right)\end{split}\]

Vemos que esta es una matriz que posee símbolos. Para poder usarla con el paquete de control, debemos pasarla a una matriz puramente numérica. esto lo haremos substituyendo los símbolos por valores

An=A.subs(sol1).subs([(b,1),(K,2),(m,3),(g,9.8)])
Bn=B.subs(sol1).subs([(b,1),(K,2),(m,3),(g,9.8)])

Ahora veamos los resultados

An

\[\begin{split}\displaystyle \left[\begin{matrix}- \frac{1}{3} & -12.2722931550313\\1 & 0\end{matrix}\right]\end{split}\]

Bn

\[\begin{split}\displaystyle \left[\begin{matrix}\frac{1}{3}\\0\end{matrix}\right]\end{split}\]

Analicemos un poco que son Bn y An

type(An)

sympy.matrices.dense.MutableDenseMatrix

Esto nos dice que es un objeto de tipo simbólico. Para poder usarlo aún debemos pasarlo a un tipo numérico.

Utilización numérica de los resultados simbólicos

Show code cell source Hide code cell source

import numpy as np
import control as ctrl
import matplotlib.pyplot as plt
# descomentar la siguiente linea para ver la imagen e una ventana emergente
# %matplotlib qt5

A1 = np.float64(An)
B1 = np.float64(Bn)

Chequeemos ahora el tipo de datos de la matriz A1:

type(A1)

numpy.ndarray

Vemos que ahora es de tipo ndarray de numpy, que es software de algebra numérico (no simbólico). Este tipo de datos es aceptado por el paquete de control, por lo que podemos usar las matrices A1 y B1 para definir nuestro sistema en espacio de estados.

sys = ctrl.ss(A1,B1,[0,1],0)

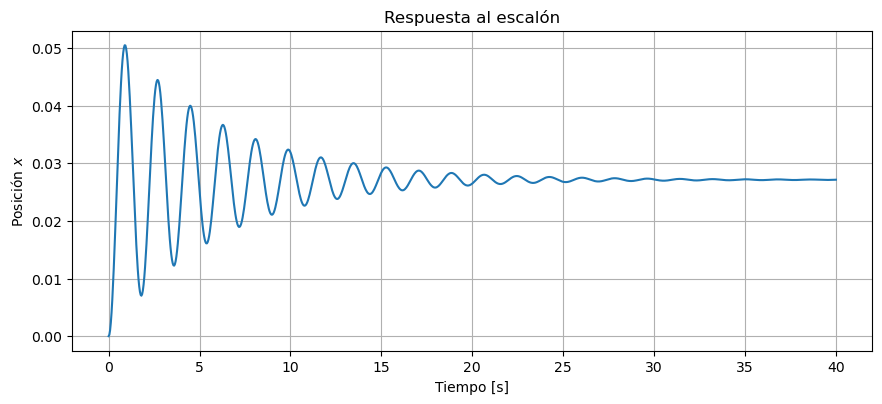
Con este modelo podemos fácilmente simular la respuesta al escalón

t,y = ctrl.step_response(sys, T=np.linspace(0,40,1000))

Ahora utilizaremos lo visto en el cuaderno de figuras

Show code cell source Hide code cell source

fig = plt.figure(figsize=(10, 4))
ax = fig.add_axes([0.1, 0.1, 0.8, 0.8])
ax.plot(t,y)
ax.set_title('Respuesta al escalón')
ax.set_xlabel('Tiempo [s]')
ax.set_ylabel('Posición $x$');
ax.grid()

Simulación No-Lineal

Primero debemos definir el sistema no lineal en una función para que después podamos integrarlo con los métodos de integración del paquete scipy (otro paquete más de Python).

def resorte_no_lineal(t, x, b=1, m=3, K=2, g=9.8, step_amp=1):
    F=1+step_amp # Hacemos la entrada igual a 2 ya que al sistema lineal le aplicamos 
                 # un escalón unitario sobre el punto de trabajo que era F=1
    x1,x2 = x
    dx1 = -b/m*x1-K/m*x2**3+F/m+g
    dx2 = x1
    return dx1, dx2

Para comenzar necesitamos también los valores numéricos de las condiciones iniciales

x0 = np.float64(sol1[x1].subs([(b,1),(K,2),(m,3),(g,9.8)])), np.float64(sol1[x2].subs([(b,1),(K,2),(m,3),(g,9.8)]))
x0

import scipy.integrate as integ
tspan = (0, 40)
t1= np.linspace(*tspan, 1000)

def simulate():
    r = integ.solve_ivp(resorte_no_lineal, tspan, x0, t_eval=t1)
    return r.y

x1,x2 = simulate()

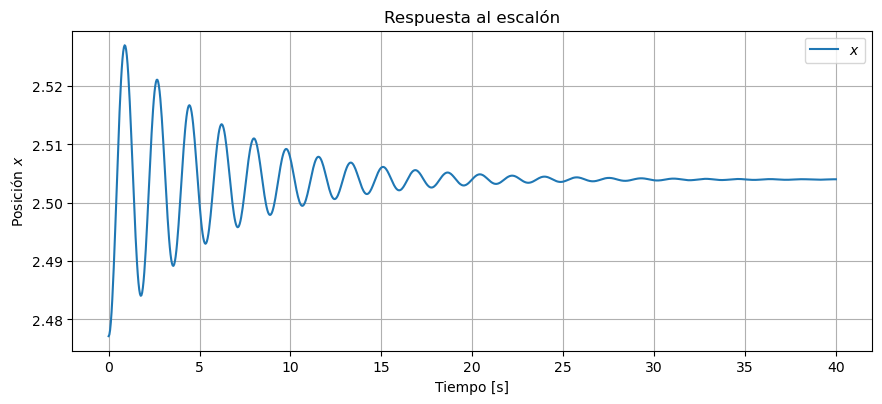
Ahora veamos los resultados de la simulación del sistema no lineal

Show code cell source Hide code cell source

fig = plt.figure(figsize=(10, 4))
ax = fig.add_axes([0.1, 0.1, 0.8, 0.8])
ax.plot(t1,x2, label='$x$')
ax.set_title('Respuesta al escalón')
ax.set_xlabel('Tiempo [s]')
ax.set_ylabel('Posición $x$')
ax.legend()
ax.grid();

Para poder evaluar las diferencias me falta agregarle a la salida del sistema lineal el valor de equilibrio.

yc = y+x0[1]

Show code cell source Hide code cell source

fig = plt.figure(figsize=(10, 4))
ax = fig.add_axes([0.1, 0.1, 0.8, 0.8])
ax.plot(t,yc, label=r'$x$ del sistema linealizado')
ax.plot(t1, x2, label=r'$x$ del sistema no lienal', alpha=0.6)
ax.set_title('Respuesta al escalón')
ax.set_xlabel('Tiempo [s]')
ax.set_ylabel('Posición $x$')
ax.legend()
ax.grid();

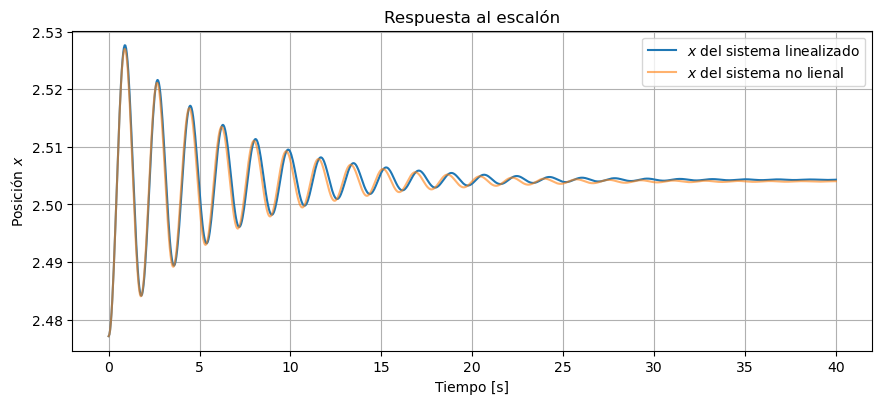
Podemos ver que la respuesta al escalón del sistema lineal y del sistema no lineal dan bastante parecidos.

Dejamos como ejercicio al lector evaluar que sucede si el escalón es más grande (5 o 10 veces más grande).