Ecuaciones de Cinética Puntual

Ecuaciones de cinética de un reactor nuclear

Las ecuaciones de cinética puntual del núcleo de un reactor a un grupo de energía y a un grupo de precursores sin fuente de neutrones son:

\[\begin{split} \begin{eqnarray} \frac{dn(t)}{dt}&=&\frac{\rho(t)-\beta}{\Lambda}n(t)+\lambda c(t)\\ \frac{dc(t)}{dt}&=&\frac{\beta}{\Lambda}n(t)-\lambda c(t) \end{eqnarray} \end{split}\]

con \(n\) el flujo neutrónico normalizado (en realidad es población de neutrones, pero bajo ciertas condiciones se puede considerar proporcional al flujo neutrónico o potencia nuclear), \(c\) la concentración de precursores, y \(\rho\) la reactividad introducida en el mismo por las barras de control. Los parámetros del sistema son: \(\Lambda = 1,76e^{-4} s\) (tiempo de reproducción de los neutrones rápidos), \(\lambda = 0,076 1/s\) (constante de decaimiento de los precursores) y \(\beta = 765\)pcm (fracción de neutrones retardados que son emitidos por los precursores).

import sympy as sp
sp.init_printing()
n, r, b, L, l, c = sp.symbols('n, rho, beta, Lambda, lambda, c')

Definimos las ecuaciones de estados, es decir, las derivadas de las variables de estados en función de los estados y las entradas.

dn=(r-b)/L*n+l*c
dn

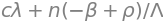
dc=b/L*n-l*c
dc

Ahora le decimos a sympy que lo represente en forma matricial:

s=sp.Matrix([dn,dc]) #las ecuaciones de estados
s

\[\begin{split}\displaystyle \left[\begin{matrix}c \lambda + \frac{n \left(- \beta + \rho\right)}{\Lambda}\\- c \lambda + \frac{\beta n}{\Lambda}\end{matrix}\right]\end{split}\]

x=sp.Matrix([n,c]) #definimos el vector de estados
x

\[\begin{split}\displaystyle \left[\begin{matrix}n\\c\end{matrix}\right]\end{split}\]

u=sp.Matrix([r]) #definimos el vector de entradas
u

\[\displaystyle \left[\begin{matrix}\rho\end{matrix}\right]\]

Linealización utilizando SymPy

Recordando la función Jacobiano, podemos valernos de esta para linealizar el sistema

A=s.jacobian(x) # la matriz A del espacio de estados
B=s.jacobian(u) #la matriz B del espacio de estados

A

\[\begin{split}\displaystyle \left[\begin{matrix}\frac{- \beta + \rho}{\Lambda} & \lambda\\\frac{\beta}{\Lambda} & - \lambda\end{matrix}\right]\end{split}\]

B

\[\begin{split}\displaystyle \left[\begin{matrix}\frac{n}{\Lambda}\\0\end{matrix}\right]\end{split}\]

Finalmente evaluamos las matrices A y B en los valores de los parámetros que tenemos dados.

A.subs([(l, 0.076), (b,765e-5),(L,1.76e-4)])

\[\begin{split}\displaystyle \left[\begin{matrix}5681.81818181818 \rho - 43.4659090909091 & 0.076\\43.4659090909091 & -0.076\end{matrix}\right]\end{split}\]

B.subs([(l, 0.076), (B,765e-5),(L,1.76e-4)])

\[\begin{split}\displaystyle \left[\begin{matrix}5681.81818181818 n\\0\end{matrix}\right]\end{split}\]

Para obtener el punto de equilibrio, suponemos que trabajaremos alrededor de \(n=1\), y lo que se hace es igualar a cero las ecuaciones de la derivada.

s2=s.subs([(l, 0.076), (b,765e-5),(L,1.76e-4),(n,1)])
sol0=sp.solve(s2,(c,r))

c0=sol0[c]
r0=sol0[r]

An=A.subs([(l, 0.076), (b,765e-5),(L,1.76e-4),(n,1),(r,r0),(c,c0)])
Bn=B.subs([(l, 0.076), (b,765e-5),(L,1.76e-4),(n,1),(r,r0),(c,c0)])

Simulación numérica

from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt
# %matplotlib qt5  # descomentar para ver las figuras en ventanas emergentes

l=0.076
b=765e-5
L=1.76e-4
n0=1

def dx(t,x):
    n=x[0]
    c=x[1]
    r= r0 if t<0 else r0 -10e-5 #1000pcm para poner un valor
    dn=(r-b)/L*n+l*c
    dc=b/L*n-l*c
    return ([dn,dc])

sol = solve_ivp(dx, (0,7), (n0,c0), method='BDF')
t= sol.t
n=sol.y[0]
c=sol.y[1]

La simulación dinámica del sistema lineal la podemos hacer usando directamente el módulo de control.

import control as ctrl
import numpy as np

Cn=np.eye(2)
Dn=np.zeros((2,1))

sys = ctrl.ss(An,Bn,Cn,Dn)
t2,y2 = ctrl.step_response(sys, T=np.linspace(0,7,1001))

Entonces ahora podemos visualizar los resultados en las siguientes figuras:

Show code cell source Hide code cell source

fig = plt.figure(figsize=(10,4))
ax = fig.add_axes([0.1, 0.1, 0.8, 0.8])
ax.plot(t,n,'r', label='Modelo no lineal')
ax.plot(t2,(y2[0,:]*-10e-5+n0).T,'b', alpha=0.6, label='Modelo lineal')
ax.grid()
ax.legend()
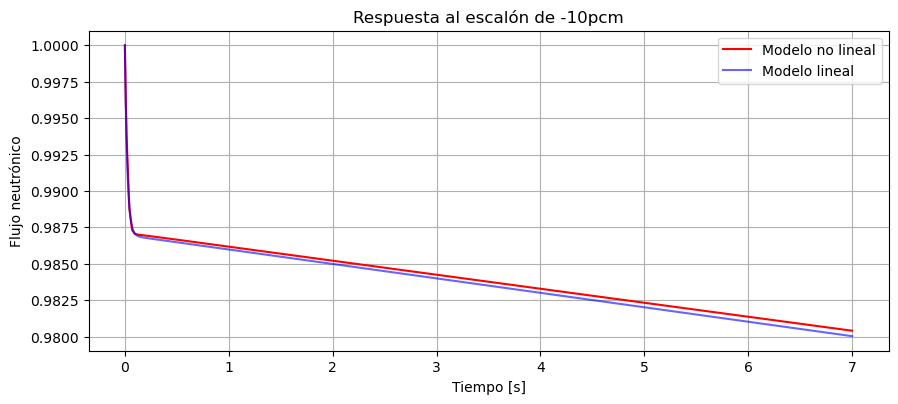
ax.set_title('Respuesta al escalón de -10pcm')
ax.set_xlabel('Tiempo [s]')
ax.set_ylabel('Flujo neutrónico');

Show code cell source Hide code cell source

fig = plt.figure(figsize=(10,4))
ax = fig.add_axes([0.1, 0.1, 0.8, 0.8])
ax.plot(t,c,'r', label='Modelo no lineal')
ax.plot(t2,(y2[1,:]*-10e-5+c0).T,'b', alpha=0.6, label='Modelo lineal')
ax.grid()
ax.legend()
ax.set_title('Respuesta al escalón de -10pcm')
ax.set_xlabel('Tiempo [s]')
ax.set_ylabel('Concentración de precursores');

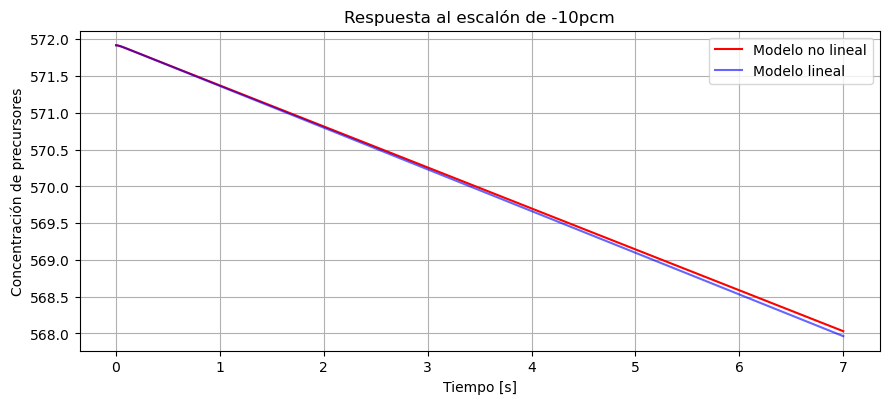
Vemos que el sistema linealizado es una muy buena aproximación del no lineal. Esto es por que la perturbación de 10pcm es suficientemente chica y el sistema no se aleja demasiado del punto del cual linealizamos.

Probemos aumentado un poco más la reactividad de entrada a 200 pcm

def dx(t,x):
    n=x[0]
    c=x[1]
    r= r0 if t<0 else r0 -200e-5 #1000pcm para poner un valor
    dn=(r-b)/L*n+l*c
    dc=b/L*n-l*c
    return ([dn,dc])

sol = solve_ivp(dx, (0,7), (n0,c0), method='BDF')
t= sol.t
n=sol.y[0]
c=sol.y[1]

Y los resultados los vemos en las siguientes gráficas:

Show code cell source Hide code cell source

fig = plt.figure(figsize=(10,4))
ax = fig.add_axes([0.1, 0.1, 0.8, 0.8])
ax.plot(t,n,'r', label='Modelo no lineal')
ax.plot(t2,(y2[0,:]*-200e-5+n0).T,'b', alpha=0.6, label='Modelo lineal')
ax.grid()
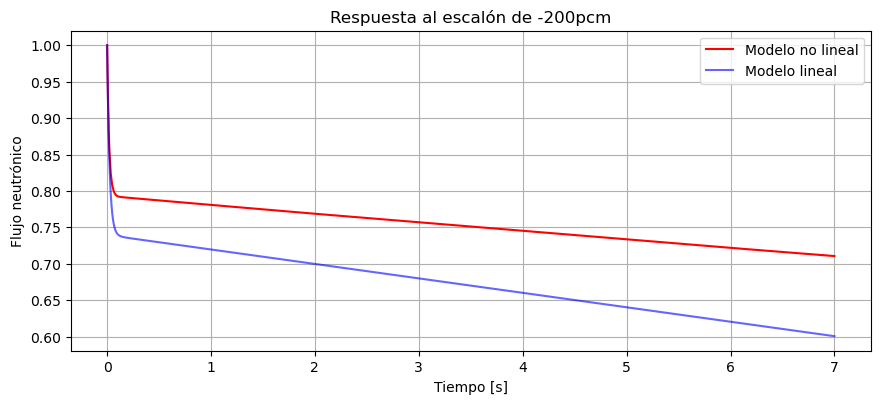
ax.set_title('Respuesta al escalón de -200pcm')
ax.set_xlabel('Tiempo [s]')
ax.legend()
ax.set_ylabel('Flujo neutrónico');

Show code cell source Hide code cell source

fig = plt.figure(figsize=(10,4))
ax = fig.add_axes([0.1, 0.1, 0.8, 0.8])
ax.plot(t,c,'r', label='Modelo no lineal')
ax.plot(t2,(y2[1,:]*-200e-5+c0).T,'b', alpha=0.6, label='Modelo lineal')
ax.grid()
ax.set_title('Respuesta al escalón de -200pcm')
ax.set_xlabel('Tiempo [s]')
ax.legend()
ax.set_ylabel('Concentración de precursores');

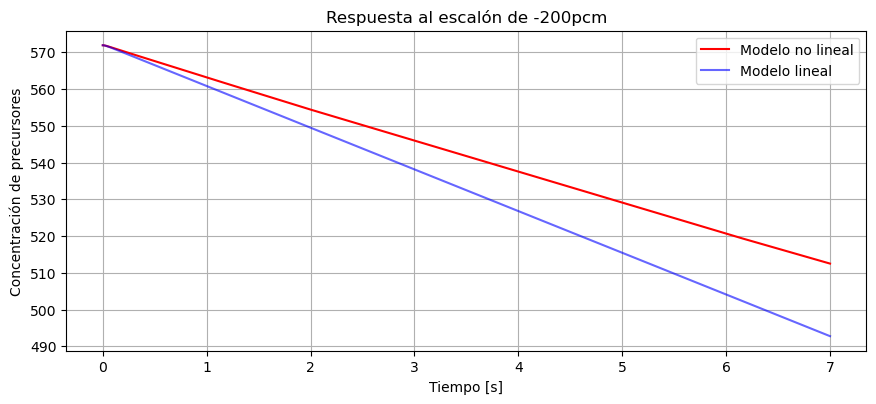
Vemos como ahora la aproximación es bastante peor a la que teníamos cuando lo perturbamos con 10 pcm.