Sensibilidad

Definición

Según Bode,la sensibilidad de la función de transferencia \(T\) con respecto al parámetro \(C\) la definimos como la variación relativa de la función \(T\) (causada por la variación de \(C\)) , dividida la variación relativa de \(C\):

\[ \text{Sensibilidad} = \dfrac{\dfrac{\Delta T}{T}}{\dfrac{\Delta C}{C}} \]

Llevando las variaciones a valores tendiendo a cero, se puede definir de forma diferencial a la sensibilidad:

\[ S^T_C = \dfrac{C}{T}\dfrac{dT}{dC}\]

Mostramos un sistema a lazo abierto y lazo cerrado. Comparemos la sensibilidad para estos dos casos:

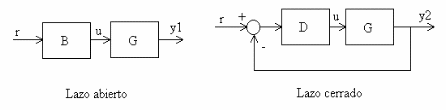
Figura 35 Lazo abierto versus lazo cerrado

En el caso de lazo abierto tenemos:

\[ Y_1(s) = G(s)B (s)R(s),\]

y por lo tanto un cambio en \(B\) o en \(G\), afecta proporcionalmente a la salida.

En el caso de lazo cerrado:

\[ Y_2( s ) = \dfrac{G(s)D(s)}{1+G(s)D(s)}R(s)\]

y por lo tanto un cambio en \(D\) o en \(G\), serán atenuados si \(\left|DG\right|\) se hace mucho mayor que la unidad.

Ejemplo

Supongamos tener el mismo sistema de control de velocidad del ejemplo anterior, del cual suponemos que la constante \(K_0\) del motor tiene un error en \(\delta K_0\). Entonces tenemos:

Lazo abierto:

La velocidad a la salida será:

\[\omega = (K_0+\delta K_0)\frac{1}{K_0}\omega_d = \left(1+\dfrac{\delta K_0}{K_0}\right)\omega_d\]

Por lo tanto el error sería \(\delta \omega = \dfrac{\delta K_0}{K_0}\omega_d\)

En términos porcentuales: \(\dfrac{\delta \omega}{\omega_d} = \dfrac{\delta K_0}{K_0}\)

Lo que indica que un error del \(10\%\) en el valor de \(k_0\) se traduce en un error del \(10\%\) en el error de la velocidad \(\omega\).

Lazo cerrado:

La velocidad a la salida será:

\[\omega = \dfrac{(K_0+\delta K_0)K_{cc}}{1+(K_0+\delta K_0)K_{cc}} \omega_d = \dfrac{(K_0+\delta K_0)K_{cc}}{1+K_0K_{cc}+\delta K_0K_{cc}}\omega_d\]

\[\omega = \dfrac{\dfrac{K_0K_{cc}}{1+K_0K_{cc}}+\dfrac{\delta K_0K_{cc}}{1+K_0K_{cc}}}{1+\dfrac{\delta K_0K_{cc}}{1+K_0K_{cc}}}\]

Si tomanos que \(\dfrac{\delta K_0K_{cc}}{1+K_0K_{cc}}\) es pequeño, y teniendo la relación \(\dfrac{1}{1+x}\approx 1 - x\) para \(x\) pequeños, entonces:

\[\omega = \left(\dfrac{K_0K_{cc}}{1+K_0K_{cc}}+\dfrac{\delta K_0K_{cc}}{1+K_0K_{cc}}\right)\left({1-\dfrac{\delta K_0K_{cc}}{1+K_0K_{cc}}}\right)\omega_d\]

Ignorando la segunda potencia de \(dK_0\) y definiendo \(\omega^\prime = \dfrac{K_0K_{cc}}{1+K_0K_{cc}}\omega_d\) (que es la velocidad no perturbada), obtenemos:

\[\omega = \omega^\prime+ \omega^\prime\dfrac{1}{1+K_0K_{CC}}\dfrac{\delta K_0}{K_0}\]

Por lo tanto:

\[\dfrac{\delta \omega^\prime}{\omega^{\prime}}=\dfrac{1}{1+K_0K_{cc}}\dfrac{\delta K_0}{K_0}\]

Que equivale decir que un cambio en un \(10\%\) en el valor de \(K_0\), solo afectará en \(\dfrac{1}{1+K_0K_{cc}}\)en \(\omega^\prime >>\omega_d\) y esto lo podemos hacer chico si \(K_{cc} K_0 >> 1\).

Aplicando la segunda definición de sensibilidad, obtendremos el mismo resultado.

Conclusión

El error en la salida controlada con realimentación es sustancialmente menos sensible a las variaciones de parámetros del sistema que en un controlador de lazo abierto. Por lo tanto no se requiere un conocimiento preciso de las características del sistema, para lograr un control preciso.