Estabilidad en Frecuencia

Introducción

Considerando el sistema a lazo cerrado

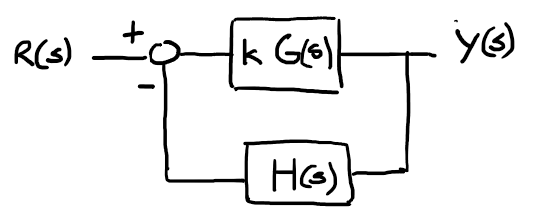
Figura 74 Diagrama de Nyquist de \(L(j\omega)\)

con función de transferencia:

\[ T(s)=\frac{Y(s)}{R(s)}= \frac{kG(s)}{1+kG(s)H(s)}= \frac{kG(s)}{1+L(s)} \]

donde \(L(s)\) es la función de transferencia de lazo o lo que es lo mismo

\[ \begin{matrix} T(j\omega)=\frac{kG(j\omega)}{1+kG(j\omega)H(j\omega)}= \frac{kG(j\omega)}{\underbrace{1+L(j\omega)}_{\text{polos a LC}}} & \Longrightarrow & 1+L(j\omega)=0 \end{matrix} \]

de lo anterior, con \(k>0\), se deduce la condición de estabilidad cuando:

\[ \begin{matrix} |kG(j\omega)H(j\omega)|<1 & \text{ a } & \angle{G(j\omega)H(j\omega)}=-180º \end{matrix} \]

esto es para sistemas que cruzan solo una vez la magnitud \(||=1\) (son los casos comunes)

Hay sistemas que al incrementar la ganancia pueden pasar de inestables a estables, en tal caso la condición de estabilidad es:

\[ \begin{matrix} |kG(j\omega)H(j\omega)|>1 & \text{ y } & \angle{G(j\omega)H(j\omega)}=-180º \end{matrix} \]

Esto es, cuando cortan más de una vez el eje \(||_{dB}=0\). Para despejar dudas es recomendable hacer un diagrama del lugar de las raíces y verificar la estabilidad, o es posible despejar las dudas al hacer un tratamiento más riguroso usando el criterio de estabilidad de Nyquist.

Criterio de estabilidad de Nyquist

A partir de una representación polar de la función de transferencia armónica del sistema:

\[ L(j\omega) \equiv L(s)|_{s=j\omega}= |L(j\omega)|e^{j\phi(\omega)} \]

con \(\phi(\omega)=\angle{L(j\omega)}\), donde:

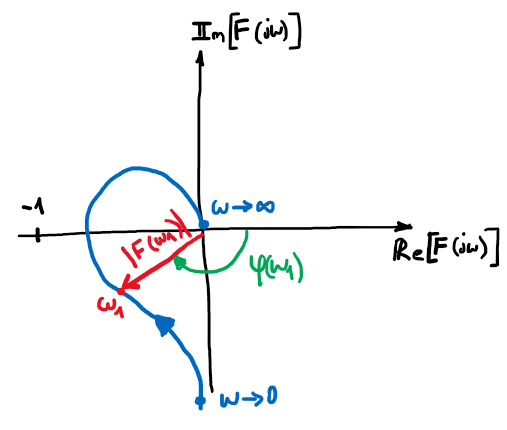
Figura 75 Diagrama de Nyquist de \(L(j\omega)\)

El criterio de estabilidad permite determinar la estabilidad del sistema en lazo cerrado a partir del diagrama de Nyquist a lazo abierto de \(L(j\omega)\)

El criterio de estabilidad de Nyquist se basa en el principio del argumento del análisis complejo.

Principio de argumento

El mapeo de un contorno cerrado de una función compleja solo puede encerrar el origen, si el contorno contiene una singularidad (lo que nosotros llamamos, polo o cero) de la función.

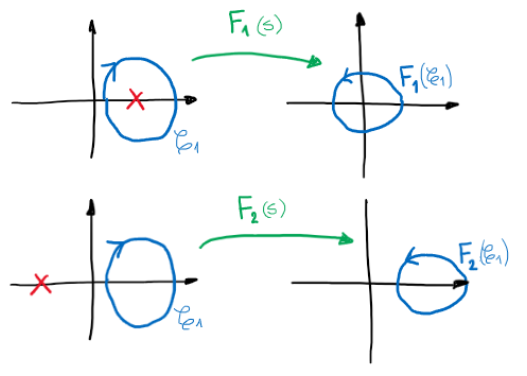
Figura 76 Diagrama de Nyquist de \(L(j\omega)\)

Mapeo de contornos

El mapeo del contorno de una función de transferencia \(L(s)\) es el camino cerrado descrito por \(L(s)\) en el plano complejo, cuando la variable \(s\) recorre un contorno ( o camino) cerrado en el plano complejo «\(s\)»

Supongamos el ejemplo genérico:

\[ L_1(s)= k \frac{(s-z_1)(s-z_2)}{(s-p_1)(s-p_2)} \]

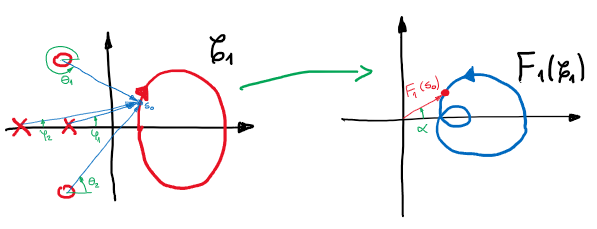
Figura 77 Diagrama de Nyquist de \(L_1(j\omega)\)

donde

\[ \alpha \equiv \angle{L_1(s_0)}= \theta_1+\theta_2+\phi_1+\phi_2 \]

cuando «\(s\)» recorre la curva \(\mathscr{C}_1\) en sentido horario, el ángulo \(\alpha\) de \(L_1(s)\) cambia, pero no hay un cambio neto de \(360º\) siempre que no haya un polo o cero de \(L_1(s)\) en el interior de \(\mathscr{C}_1\). En este caso, el mapeo del contorno de \(L_1(s)\) no incluye el origen.

consideremos ahora \(L_2(s)\) como se muestra:

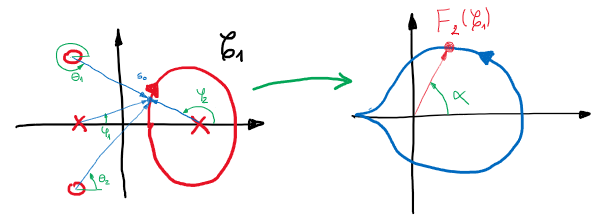
Figura 78 Mapeo de la curva \(\mathscr{C}_1\) para \(L_2(s)\)

En este caso como hay una singularidad de \(L_2(s)\) dentro del contorno \(\mathscr{C}_1\). Cuando «\(s\)» recorre \(\mathscr{C}_1\) hay un cambio neto de \(360º\) en la fase \(\phi_2\) correspondiente a la singularidad dentro del contorno \(\mathscr{C}_1\) lo que hace que \(\alpha\) cambie \(360º\) esto significa que el mapeo encierra el origen.

Vamos a analizar la ecuación característica, por ser la que define la ubicación de los polos del sistema a lazo cerrado:

\[ f(s) =1+ kG(s)H(s)= 1+ k L(s)=0 \]

por lo que para aplicar el principio del argumento usaremos el contorno que encierra todo el semi-plano derecho, es decir, la región de inestabilidad \(\mathbb{C}^+\)

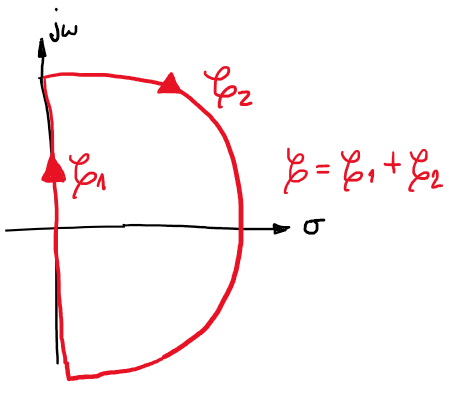
Figura 79 Contorno que encierra \(\mathbb{C}^+\)

Entonces si el mapeo de \(L(s)\) encierra el origen si el contorno \(\mathscr{C}\) encierra un número de polos y ceros tal que:

\[ N-P \not= 0 \]

donde

\[\begin{split} \begin{matrix} N = \text{ número de ceros de }L(s)\text{ en el interior de }\mathscr{C}\\ P = \text{ número de polos de }L(s)\text{ en el interior de }\mathscr{C} \end{matrix} \end{split}\]

y cuando

\[\begin{split} \begin{matrix} N > P & \Longrightarrow & \text{mapeo horario}\\ P < P & \Longrightarrow & \text{mapeo antihorario} \end{matrix} \end{split}\]

Como queremos analizar \(1+kL(s)=0\) entonces es lo mismo que analizar \(kL(s)=kG(s)H(s)\) y como punto crítico usar el \(-1\).

Criterio de estabilidad

Sea

\(N\) = número de vueltas alrededor de \(-1\) del diagrama de Nyquist de \(kG(s)H(s)\)

\(P\) = número de polos a lazo abierto en el semi-plano derecho (RHP)

\(Z\) = número de polos a lazo cerrado en el RHP

entonces $\( Z=N + P \)$

para que el sistema sea estable debe ser \(Z=0\)

Diagrama de Nyquist asintótico

Receta para dibujar un diagrama de Nyquist asintótico (No hace falta mas que esto para determinar la estabilidad):

1. Con la ayuda de un diagrama de Bode determinar la forma para \(0 \leq \omega \leq \infty\)

2. Evaluar el cierre del diagrama por infinito

3. Contar las vueltas a -1

\[\begin{split} N = \left\{ \begin{array}{l} > 0 & \Longrightarrow &\text{Horario}\\ < 0 &\Longrightarrow &\text{Antihorario} \end{array}\right. \end{split}\]

4. Determinar los polos de \(L(s)\) en el RHP, esto es P

5. Calcular la estabilidad \(\Longrightarrow ~ Z=N+P\)

Ejemplo: Diagrama de Nyquist para determinar la estabilidad

Supongamos un sistema con la siguiente función de transferencia de la que evaluaremos la estabilidad usando el criterio de Nyquist

\[ G(s)=\frac{1}{(s+1)^2} \]

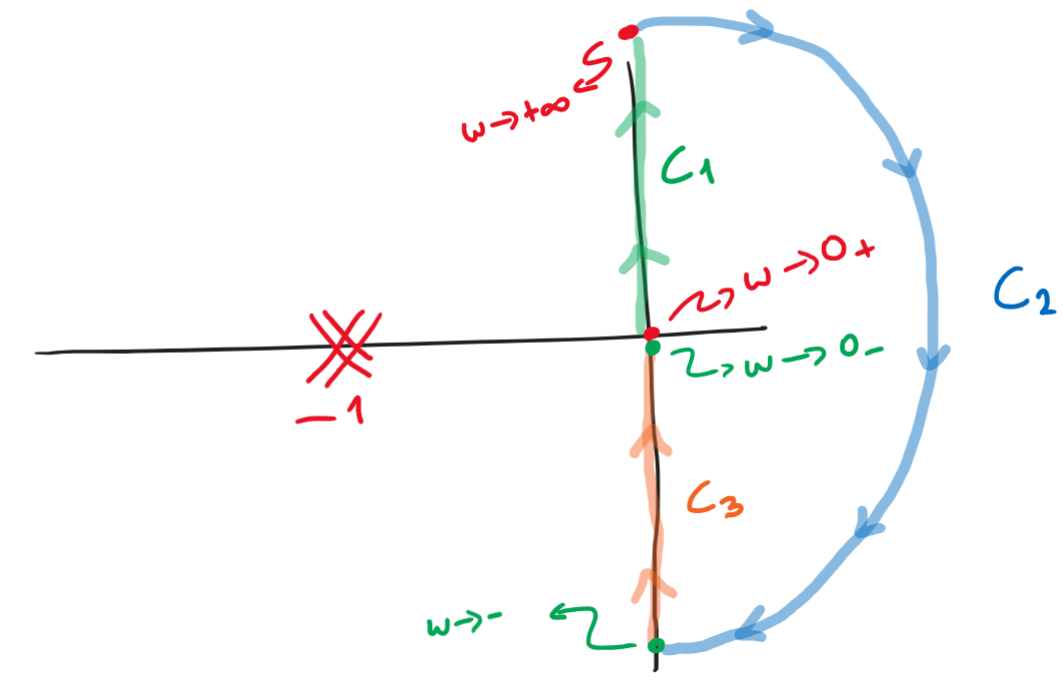
Figura 80 Curva de Nyquist en el plano-\(s\) de \(G(s)\)

1. Dibujamos un diagrama de Bode de la función de lazo \(L(s)= kG(s)\), en este caso es suficiente con un Bode asintótico.

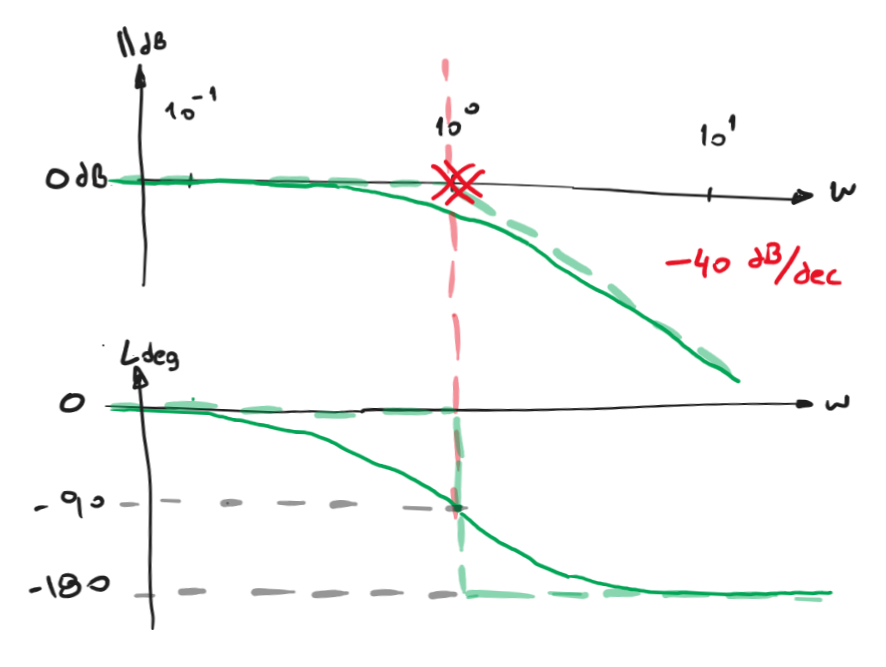
Figura 81 Diagrama de Bode asintótico de \(G(j\omega)\)

2. Con la ayuda del Bode anterior dibujamos el Nyquist para las frecuencias \(0_+ \leq \omega \leq +\infty\) y el simétrico para frecuencias negativas

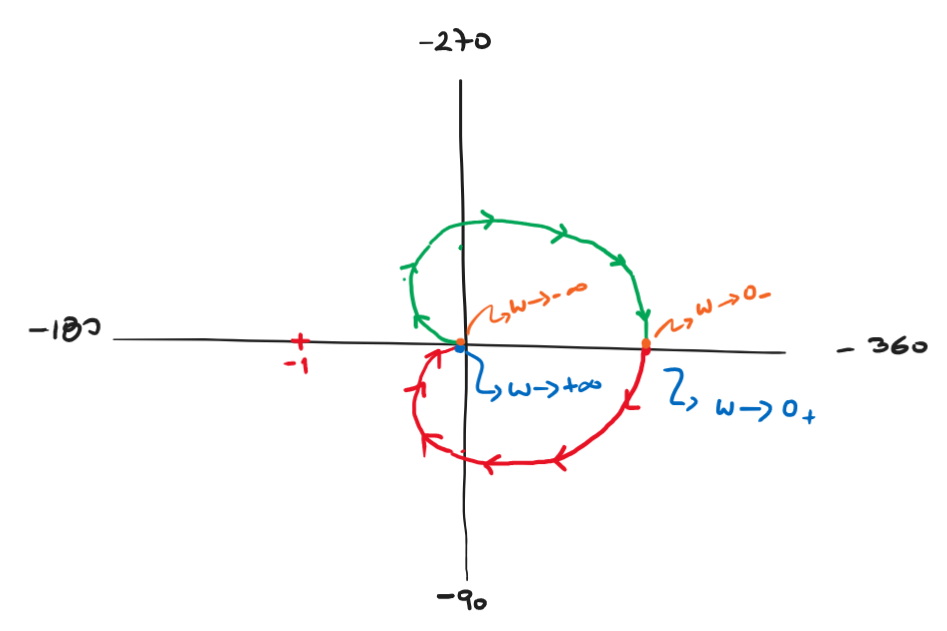
Figura 82 Diagrama de Nyquist de \(G(s)\)

3. En este caso el diagrama de Nyquist es cerrado por lo que no es necesario evaluar el cierre por infinito. Observar que todos los puntos de \(\mathscr{C}_2\) se mapean a cero del diagrama de Nyquist. \(G(\mathscr{C}_2)\) con \(s=\rho e^{-j\theta}\) con \(\rho \longrightarrow \infty\).

4. Contamos las vueltas alrededor de -1 y los polos en \(\mathbb{C}^+\) a lazo abierto, es decir polos de \(L(s)\):

\[\begin{split} \begin{matrix} N = 0 \text{ en este caso no hay vueltas sobre -1 } \forall k\\ P = 0 \text{ en este caso no hay polos de } G(s) \text{ en } \mathbb{C}^+ \end{matrix} \end{split}\]

5. Usamos el criterio de Nyquist para determinar la estabilidad del sistema es: $\( Z= N+P= 0 \)\( No hay polos en el RHP, por lo que el sistema es estable para cualquier valor de \)k$

6. Para verificar la estabilidad del sistema, dibujamos el lugar de las raíces asintótico para este sistema con realimentación unitaria y ganancia \(k\), tanto para \(k\) negativos como positivos, esto es:

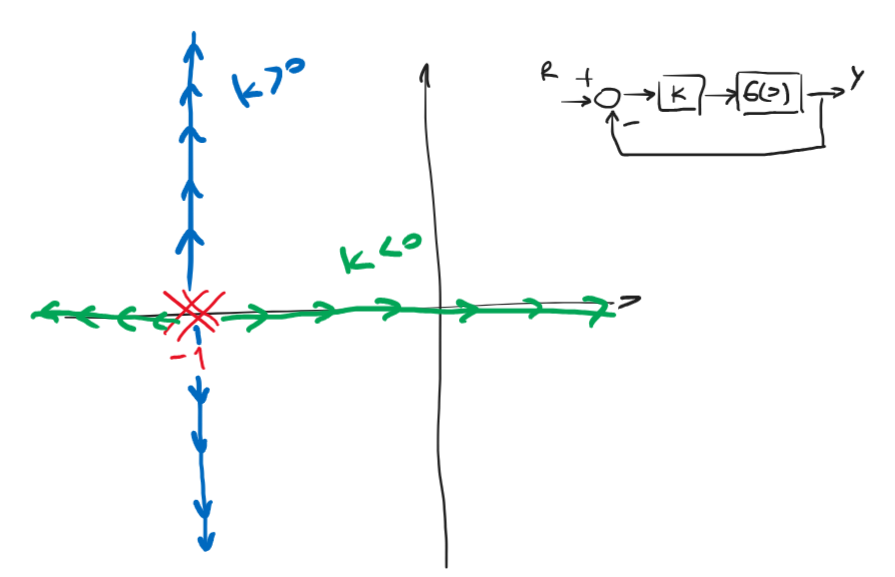
Figura 83 Lugar de las raíces asintótico de \(G(s)\)

Notar que para ciertos valores de ganancias negativas, el sistema se hace inestable con un polo en el semi-plano derecho.

Otro ejemplo: Con cierre por \(\infty\)

En este caso analizaremos un sistema en el que hay que cerrar el diagrama de Nyquist por el infinito de la función:

\[ G(s) = \frac{1}{s(s+1)} \]

Los diagramas de Nyquist cierran por \(\infty\) cuando hay singularidades sobre el eje-\(j\omega\), en estos casos hay es necesario definir de que lado esta cada singularidad, están incluidas en \(\mathbb{C}^+\) o en \(\mathbb{C}^-\), para este ejemplo, el polo en cero lo excluimos de \(\mathbb{C}_+\) por lo que \(P=0\)

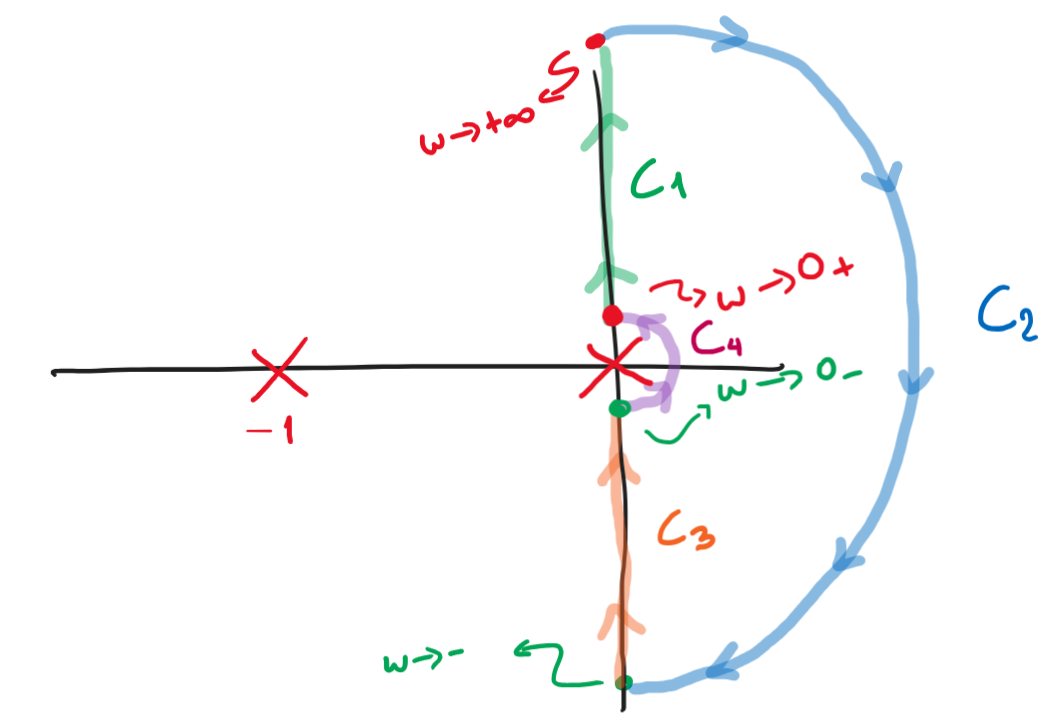
Figura 84 Curva de Nyquist en el plano-s de \(G(s)= \frac{1}{s(s+1)}\)

Comenzamos haciendo un Bode asintótico para dibujar el Nyquist para frecuencias \(\omega >0\), es decir que van entre \(0_+ < \omega < +\infty\) y el simétrico de frecuencias negativas \(0_- < \omega < -\infty\)

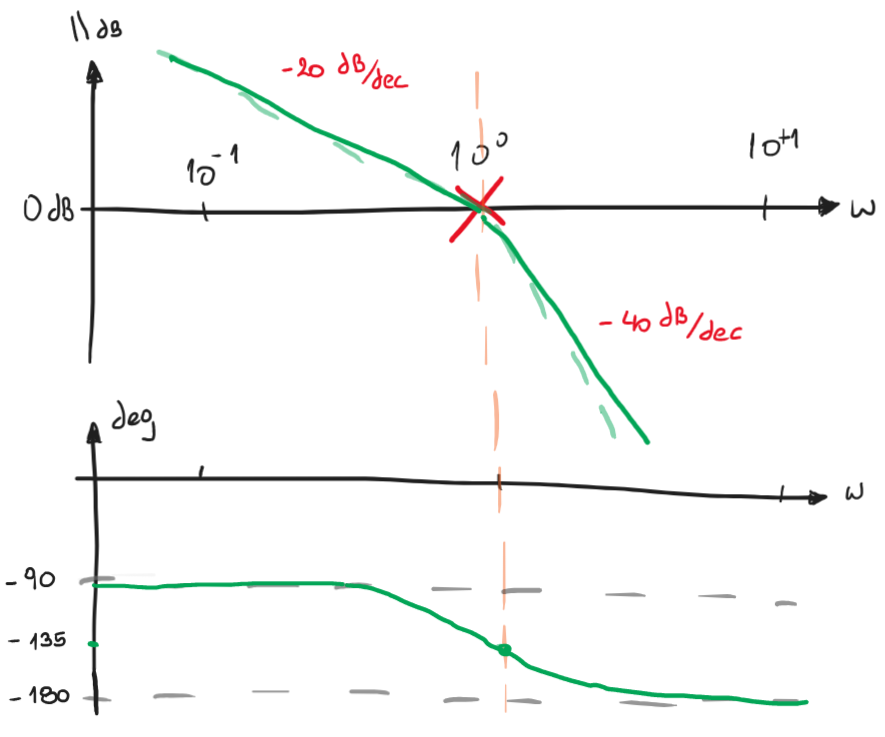
Figura 85 Bode asintótico de \(G(s)= \frac{1}{s(s+1)}\)

Con el Bode anterior dibujamos el mapeo de \(G(\mathscr{C}_1)\)

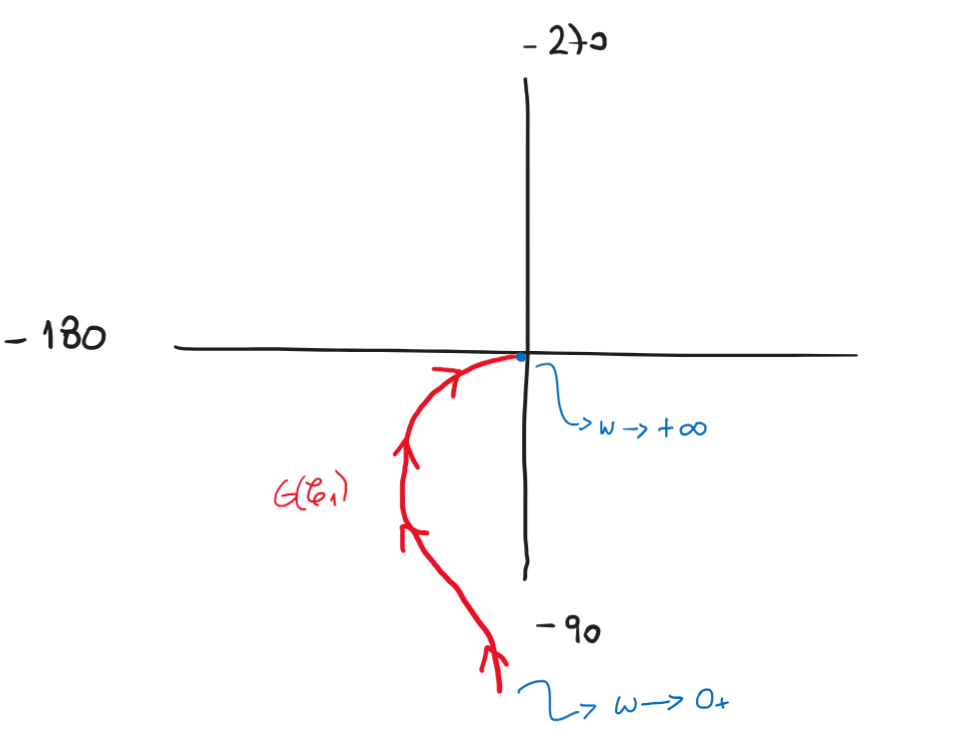
Figura 86 Nyquist de \(G(\mathscr{C}_1)\)

El mapeo de \(G(\mathscr{C}_2)\) donde \(\mathscr{C}_2: s=\rho e^{j\theta} \text{ con } \rho \longrightarrow \infty \text{ y } -\frac{\pi}{2}<\theta<\frac{\pi}{2}\) pasando por \(\theta = 0\) son puntos que van a parar al 0 del diagrama de Nyquist.

\[ G(s)= \lim_{\rho \rightarrow \infty}\frac{1}{\rho e^{j\theta}(\rho e^{j\theta}+1)}\approx \lim_{\rho \rightarrow \infty} \frac{1}{\rho} e^{-j\theta} \]

Agregamos a lo que dibujamos para frecuencias positivas \(\omega>0\) a partir del Bode, y el simétrico para frecuencias negativas, es decir \(\omega<0\).

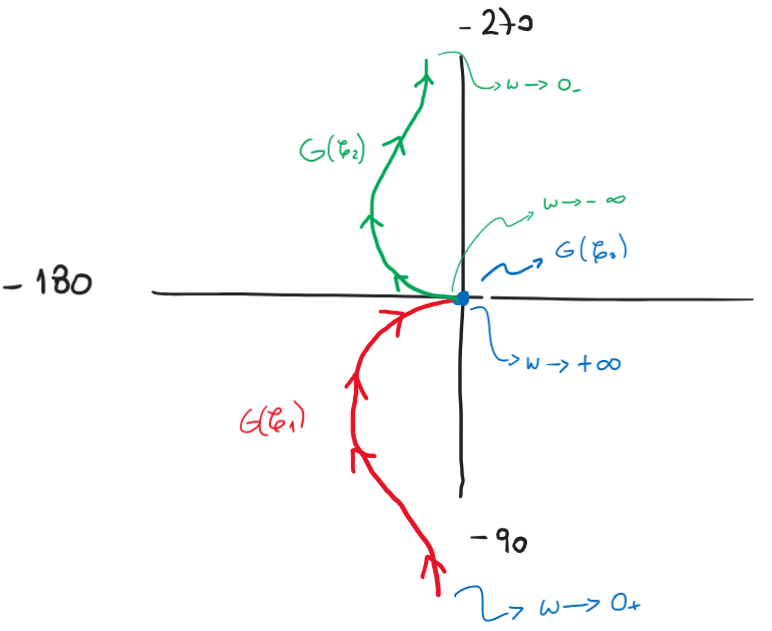
Figura 87 Nyquist de \(G(s)\) sin cerrar

Analizamos el cierre por infinito, para lo que usaremos el contorno \(\mathscr{C}_3\), que se parametriza como: $\( \mathscr{C}_3: s=\rho e^{j\theta} \text{ con } \rho \longrightarrow 0 \text{ y } -\frac{\pi}{2}<\theta<\frac{\pi}{2} \text{ pasando por }\theta = 0 \)$

Sustituyendo en \(G(s)\)

\[ G(s)= \lim_{\rho \rightarrow 0}\frac{1}{\rho e^{j\theta}(\rho e^{j\theta}+1)}\approx \lim_{\rho \rightarrow 0}\frac{1}{\rho e^{j\theta}} = \lim_{\rho \rightarrow 0} \frac{1}{\rho} e^{-j\theta} \]

De lo anterior con \(\rho \longrightarrow 0\) tenemos que el módulo del mapeo tiende a infinito \(||\longrightarrow \infty\) y si no es evidente, el ángulo lo podemos evaluar para algunos valores relevantes de \(\theta\) y calcular el argumento del mapeo, que en este caso le llamaremos \(\phi\), para lo que hacemos la siguiente Tabla 1:

Tabla 1 Mapeo del ángulo \(\theta\)

\(\theta [deg]\)	\(\phi [deg]\)
-90	90
-45	45
0	0
45	-45
45	-45

Con lo anterior podemos cerrar el diagrama como se ve en Figura 88

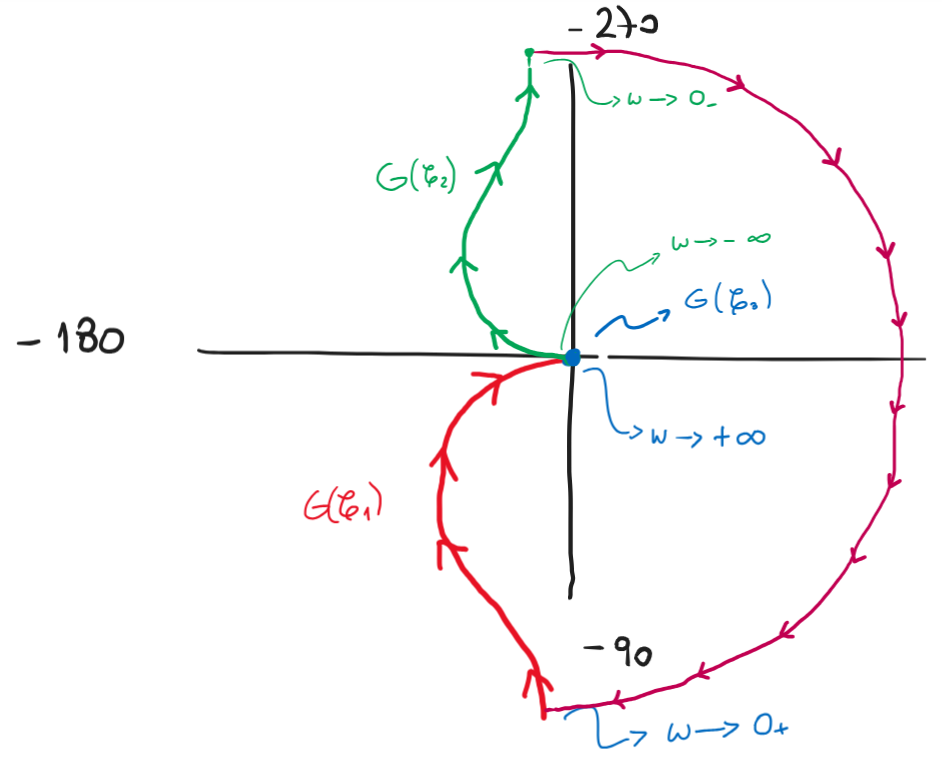
Figura 88 Nyquist de \(G(s)\) cerrado

Finalmente con el diagrama cerrado podemos, contamos la vueltas al -1 y los polos de \(G(s)\) en el RHP y calculamos la estabilidad del sistema:

\[ \begin{matrix} N=0 & \text{ y } & P=0 & \Longrightarrow & Z=0 ~~ \forall k>0 \text{( siempre es estable)} \end{matrix} \]

Validamos lo anterior haciendo el lugar de las raíces asintótico para \(k>0\). En este caso el sistema tiene dos asíntotas con centro de asíntota \(\sigma_a = -0.5\) y ángulos de asíntota \(\theta_a = \pm \pi/2\). Con lo que el asintótico queda de la forma:

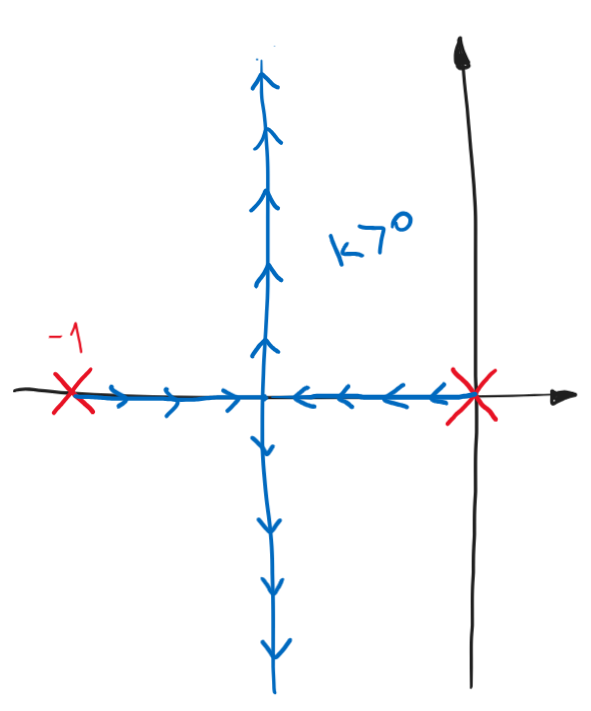
Figura 89 Lugar de las raíces asintótico de \(G(s)= \frac{1}{s(s+1)}\) con \(k>0\)

Un detalle del gráfico, «que no es relevante para determinar la estabilidad», que suele aparecer al dibujar el diagrama de Nyquist con alguna herramienta de simulación. Cuando la frecuencia es muy grande la curva de Nyquist no se hace asintótica al eje \(j\omega\) en realidad para este ejemplo, se hace asintótica al eje -1.

\[ \lim_{\omega \rightarrow 0^+} G(\omega)=\lim_{\omega \rightarrow 0^+}\bigg(\frac{-1}{\omega^2+1}-j\frac{1}{\omega(\omega^2+1)} \bigg)= -1 \]

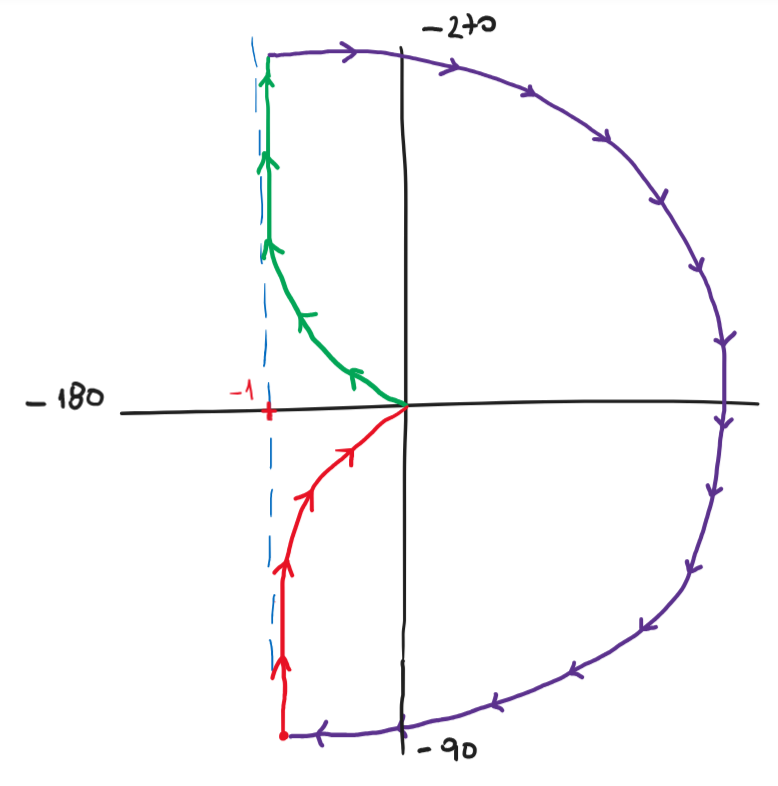
Figura 90 Asíntota de Nyquist

Todavía quedan algunas preguntas por responder sobre este problema. ¿Cómo cierra el Nyquist si incluimos el polo en la curva que encierra el semi-plano derecho? y ¿Qué sucede con la estabilidad para \(k<0\)?

Al incluir el polo dentro de la curva que encierra el semi-plano derecho, ahora los polos de \(G(s)\) en RHP son \(P=1\). Realizamos el diagrama de Nyquist para ese caso y contamos las vueltas a -1, por lo que \(N=-1\), con lo que \(Z=N+P=0\) esto es para todo \(k>0\).

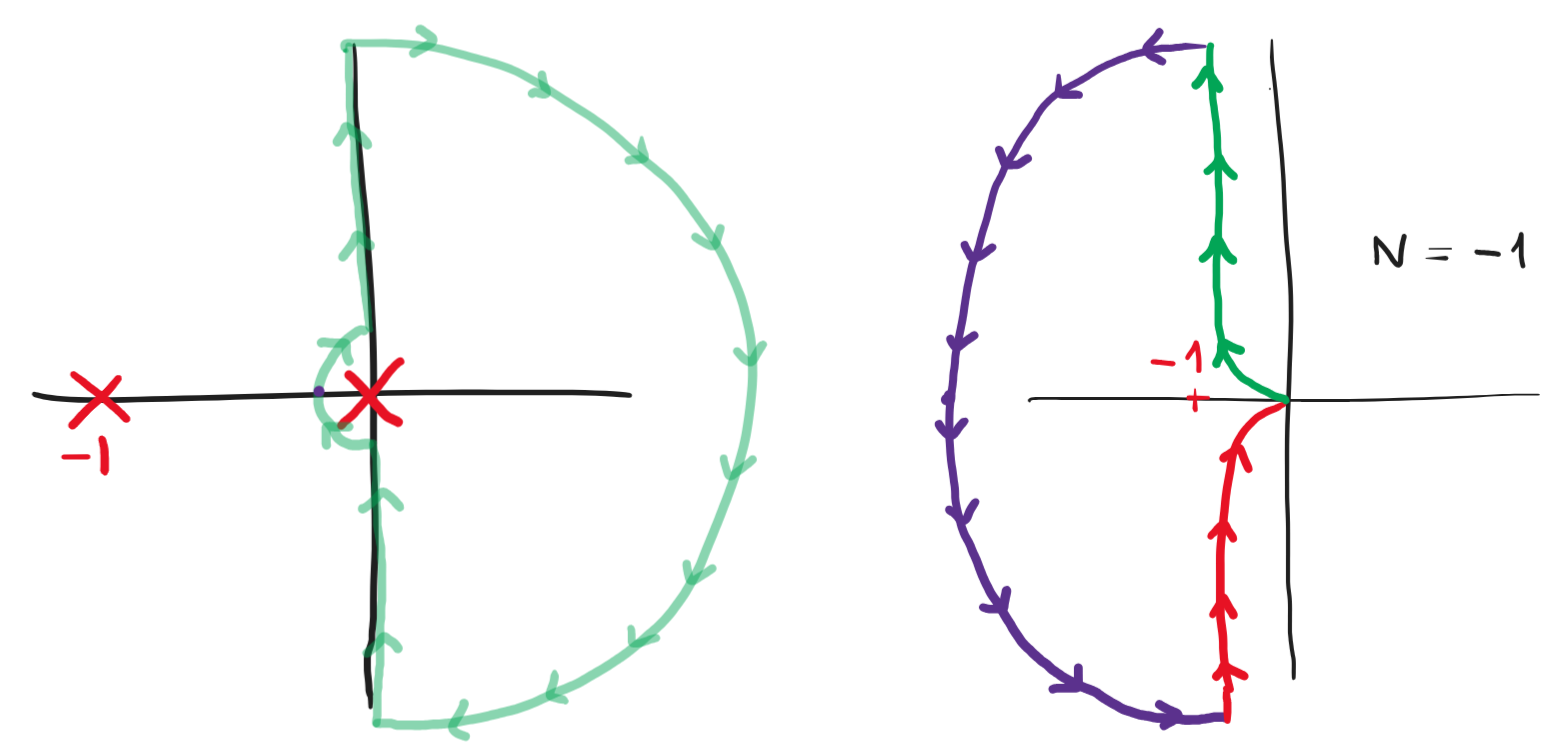
Figura 91 Nyquist cuando la curva de Nyquist contiene el polo en cero

La estabilidad para \(k<0\) se puede analizar de dos formas, por un lado se puede hacer el Nyquist para esa condición (rotando 180° el diagrama) como se muestra en la figura siguiente y analizar las vueltas a -1 del sistema.

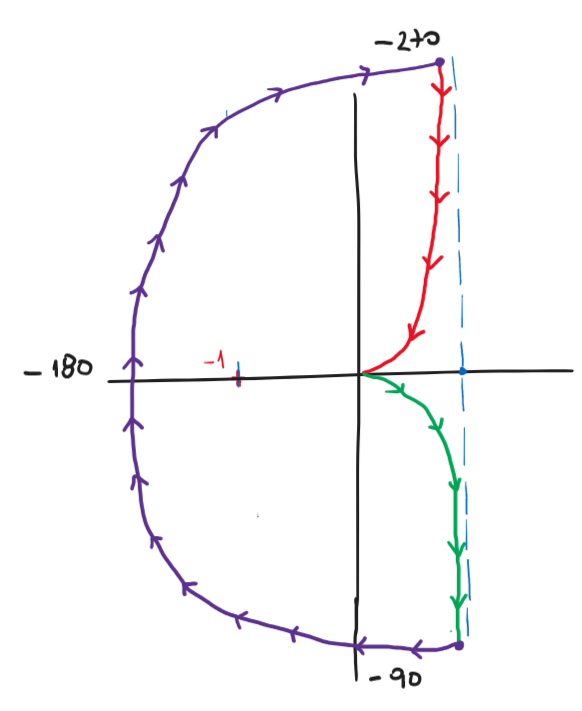
Figura 92 Nyquist de \(k<0\) y la curva de Nyquist no contiene el polo en cero.

Para este caso \(P=0\) y \(N=1\) para todo valor de \(k<0\) con lo que \(Z=N+P =1 \) por lo que el sistema es siempre inestable con un polo en RHP.

Por otro lado, lo que suele ser mas práctico, es plantear «cambiar la escala del eje real» reemplazando el punto -1 por el \(-\frac{1}{k}\), Notar que para analizar la estabilidad estamos evaluando la ecuación característica el sistema, pero ahora con \(k\) variable, es decir \(1+kL(s)=0\), por lo que es lo mismo que ver \(L(s)=-\frac{1}{k}\). Cuando \(k>0\) se mueve en el eje real negativo y cuando \(k<0\) el punto se mueve en el eje real positivo, de esta forma dibujamos el Nyquist para \(k=1\) y luego movemos el punto \(-\frac{1}{k}\) como se muestra en la figura siguiente.

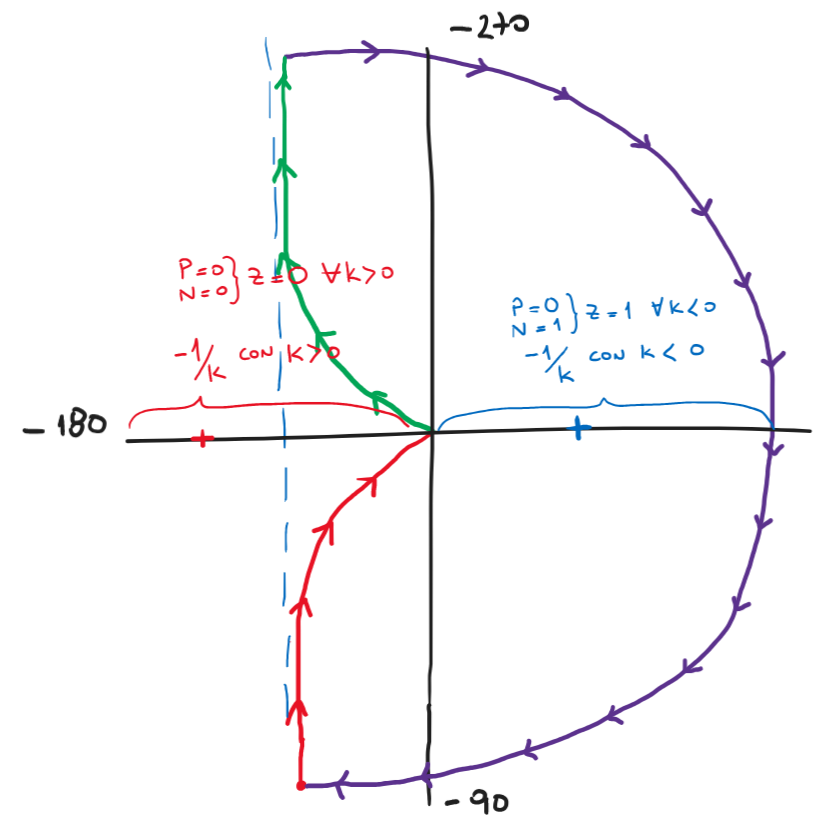
Figura 93 Análisis de estabilidad en el punto \(-\frac{1}{k}\) para todo valor de \(k\).

Margen de Fase (MF) y Margen de Ganancia (MG)

Usando diagramas de Nyquist se definen dos mediciones cuantitativas de «cuan estable es el sistema que estamos analizando». Estas son el margen de ganancia y el margen de fase. Sistemas con margenes de estabilidad de ganancia y fase grandes pueden soportar grandes variaciones en los parámetros antes de hacerse inestables. En el lugar de las raíces esto sería equivalente a cuan lejos se encuentran los polos del eje \(j\omega\).

Definición de Margen de Fase \(\Phi_M\)

Es el cambio en la ganancia a lazo abierto, expresado en decibels (\(dB\)), requerida a fase \(180º\) para hacer que el sistema sea inestable a lazo cerrado.

Definición de Margen de Fase \(G_M\)

Es el cambio de fase a lazo abierto cuando la ganancia del sistema es 1 en valor absoluto (o \(0~dB\)) que hace que el sistema a lazo cerrado sea inestable.

Gráficamente es:

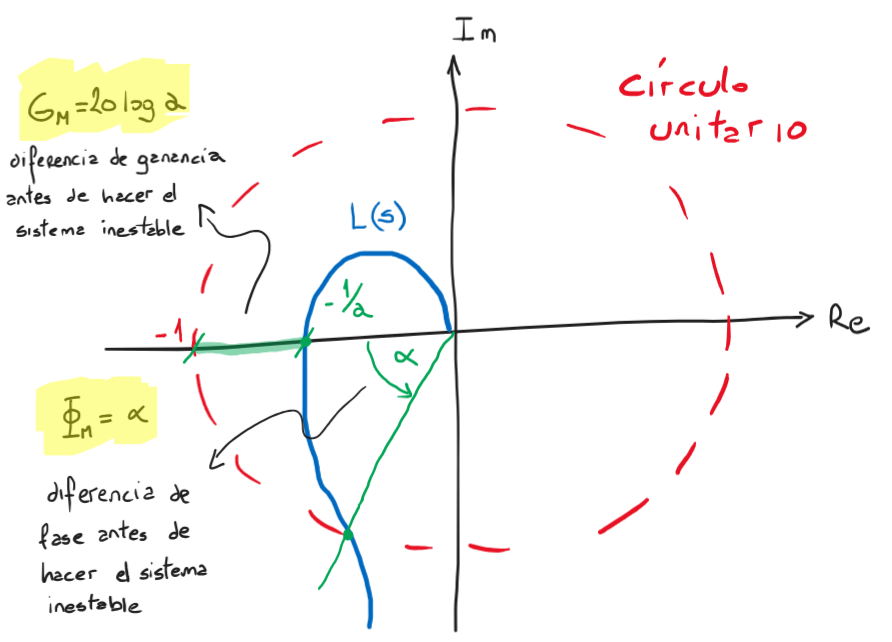
Figura 94 Margenes de estabilidad

Si la ganancia del sistema es multiplicada por \(a\) el Nyquist intercepta el punto crítico -1. Se dice que el margen de ganancia es \(a\) o expresado en decibels \(G_M=20\log(a)\).

Luego cuando la ganancia es unitario (cuando el Nyquist corta el circulo unitario). El ángulo \(\alpha\) es el margen de fase. En tal caso, si tenemos un corrimiento para dicha ganancia de \(\alpha\) grados, el sistema se hace inestable.

Ejemplo: Cálculo de Margenes de estabilidad \(\Phi_M\) y \(G_M\)

En este ejemplo vamos a calcular en forma analítica los margenes de ganancia y de fase del sistema

\[ L(s)=\frac{6}{(s^2+2s+2)(s+2)} \]

para encontrar el margen de ganancia hay que determinar donde corta el Nyquist el eje real, esto es

\[ L(j\omega) = \left.\frac{6}{(s^2+2s+2)(s+2)}\right|_{s\rightarrow j\omega} = \frac{6[4(1-\omega^2)-j\omega(6-\omega^2)]}{16(1-\omega^2)^2+\omega^2(6-\omega^2)^2} \]

es decir,

\[ L(j\omega) = \frac{6[4(1-\omega^2)]}{16(1-\omega^2)^2+\omega^2(6-\omega^2)^2} -j\frac{6[\omega(6-\omega^2)]}{16(1-\omega^2)^2+\omega^2(6-\omega^2)^2} \]

cuando \(\mathbb{I}m = 0 \Longrightarrow \omega=\sqrt{6} rad/s\) entonces \(\mathbb{R}e=-0.3 \Longrightarrow \) la ganancia puede ser incrementada (multiplicar) hasta 3.33 unidades antes de que el sistema se haga inestable

\[ G_M = 20\log{3.33}= 10.45 dB \]

El margen de fase ocurre cuando \(|L(j\omega_c)|=1\) para esto con la ayuda del software de cálculo se puede hallar la frecuencia \(\omega=\omega_c\) (corte por \(0dB\)), que para este caso es:

\[ |L(\omega)|=1 \Longrightarrow \omega_c=1.253 rad/s \]

\[ \omega_c \longrightarrow \phi= -112.3 \Longrightarrow \Phi_M=-112.3+180=67.7º \]

Margenes de estabilidad en diagramas de Bode

Gráficamente en el diagrama de Bode los margenes de estabilidad, el margen de ganancia y el margen de fase se indican como muestra la figura siguiente:

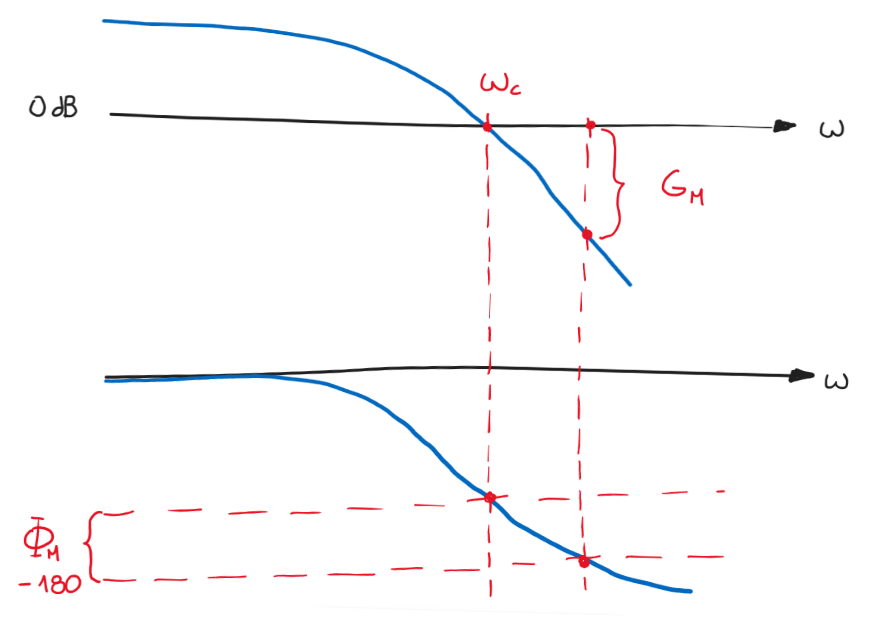
Figura 95 Margenes de estabilidad en el diagrama de Bode