Respuesta Frecuencial de Sistemas lineales y SISO

Formalismos matemáticos

Teorema

Dado \(\Sigma = (N,D)\) un sistema SISO y con \(\omega>0\). Si \(T_{N,D}\) no tiene polos en el eje imaginario, entonces dado \(u(t)=u_0 \sin(\omega t)\). hay un única salida periódica \(y_p(t)\) con periodo \(T=\dfrac{2\pi}{\omega}\) que es solución del sistema tal que:

\[ y(t) = u_0 Re(H_\Sigma) \sin(\omega t) + u_0 Im(H_\Sigma) \cos(\omega t) \]

como entrada una sinusoide \(\Longrightarrow\) salida senoide desfasado \(\therefore\) si \((N,D)\) es un sistema SISO y lineal de la forma input/output (Esto significa que no importan los estados, solo se busca una \(u(t)\) que haga satisfacer el \(y(t)\)) se define la respuesta frecuencial por \(H_{N,D}(\omega)= T_{N,D}(i\omega)\) es decir haciendo \(s=i\omega\).

También existe una correspondencia entre la respuesta frecuencial y la respuesta impulsiva.

Proposición

Sea \((N,D)\) sea un sistema estrictamente propio, SISO y lineal, de la forma input/output y supongamos que los polos de \(T_{N,D}\) están en el semiplano negativo. Entonces \(H_{N,D}(\omega) = \check{h}_{N,D}(\omega)\) la transformada de Fourier.

Demo

tenemos que \(H_{N,D}(\omega)= T_{N,D}(i\omega)\) y entonces:

\[ H_{N,D}(\omega)=\displaystyle\int_{+0}^{\infty} h_{N,D}(t)e^{i\omega t}\, dt \]

esto es la transformada de Laplace en \(s=i\omega\)

asumiendo todos los polos en el semiplano izquierdo \(\mathbb{C}^-\) tenemos que la integral existe, si ademas, consideramos \(\underbrace{h_{N,D}(t)=0\text{ para }t<0}_{causal}\) tenemos que:

\[ H_{N,D}(\omega)=\displaystyle\int_{-\infty}^{\infty} h_{N,D}(t)e^{i\omega t}\, dt = \check{h}_{N,D}(\omega) \]

Proposición

Dado \((N,D)\) un sistema estrictamente propio, SISO y lineal, de la forma input/output y suponiendo que los polos de \(T_{N,D}\) están en el semiplano izquierdo, tenemos que:

\[ T_{N,D}(s)=\dfrac{1}{2\pi}\displaystyle\int_{-\infty}^{\infty} \dfrac{H_{N,D}(\omega)}{s-i\omega}\, d\omega \]

esta es la forma de ir al dominio de Laplace desde el dominio frecuencial, es posible demostrar la preposición anterior aplicando la transformada de Fourier inversa.

Resultado importante es la correspondencia entre los tres dominios, con esto se establece una relación entre el dominio temporal, el plano-s o de Laplace y el dominio frecuencial, como se muestra en la figura siguiente:

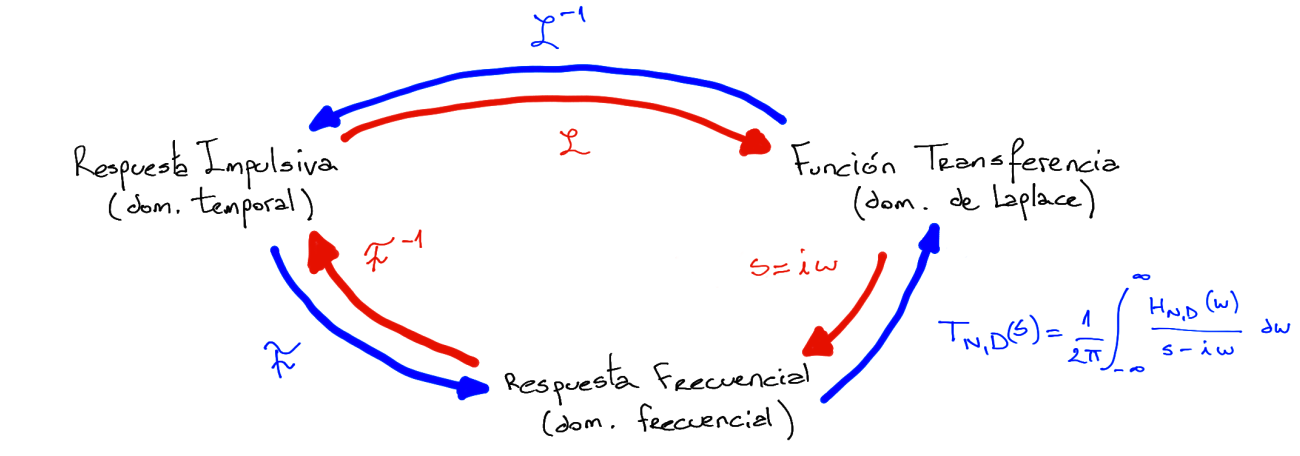
Figura 53 Relaciones entre dominios temporal, Laplace y frecuencial

Análisis del paso de \(s\rightarrow \omega\)

Seguimos analizando del paso de del dominio de Laplace al frecuencial, para esto consideraremos el sistema lineal e invariante en el tiempo descripto por la función de transferencia:

\[ H(s)= k \dfrac{\prod_{j=1}^{m}(s-z_j)}{\prod_{i=1}^{n}(s-p_i)} \]

que por simplicidad consideraremos que \(p_i\) y \(z_j\) son reales simples.

Nos interesa determinar la respuesta del sistema a una entrada de la forma (sinusoidal)

\[ u(t)= U_0 \sin(\omega t) \Longrightarrow U(s)=\dfrac{U_0\omega}{s^2+\omega^2} \]

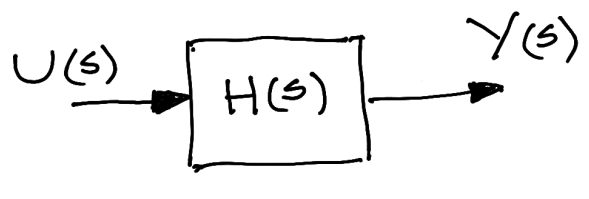
Figura 54 Sistema \(H(s)\)

asumiendo condiciones iniciales nulas

\[\begin{split} \begin{matrix} Y(s) & = & H(s)U(s)\\ & = & k \dfrac{\prod_{j=1}^{m}(s-z_j)}{\prod_{i=1}^{n}(s-p_i)}\dfrac{U_0\omega}{s^2+\omega^2} \end{matrix} \end{split}\]

expandiendo en fracciones parciales, se tiene

\[ Y(s)=\sum_{i=1}^n \dfrac{\alpha_i}{s-p_i}+\underbrace{\dfrac{\alpha_o}{s+j\omega}+\dfrac{\alpha_o^*}{s-j\omega}}_{(1)} \]

donde el calculo de los residuos da:

\[ \alpha_i= \displaystyle\lim_{s \to{p_i}}{(s-p_i)H(s)\dfrac{U_0\omega}{s^2+\omega^2}} \]

\[\begin{split} \begin{matrix} \alpha_o & = & \displaystyle\lim_{s \to{+j\omega}}{(s-j\omega)H(s)\dfrac{U_0\omega}{(s+j\omega)(s-j\omega)}}\\ &=&\dfrac{U_0\omega H(-j\omega)}{-j2\omega}=j\dfrac{U_0}{2}H(-j\omega) \end{matrix} \end{split}\]

\[\begin{split} \begin{matrix} \alpha_o^* &=& \displaystyle\lim_{s \to{j\omega}}{(s-j\omega)H(s)\dfrac{U_0\omega}{(s+j\omega)(s-j\omega)}}\\ &=&\dfrac{U_0\omega H(j\omega)}{j2\omega}=-j\dfrac{U_0}{2}H(j\omega) \end{matrix} \end{split}\]

de \((1)\) tenemos que:

\[\begin{split} \begin{matrix} (1)&=& \dfrac{\alpha_o(s-j\omega)+\alpha_o^*(s+j\omega)}{s^2+\omega^2}=\dfrac{s(\alpha_o+\alpha_o^*)+j\omega(\alpha_o+\alpha_o^*)}{s^2+\omega^2}\\ &=&\dfrac{-j\dfrac{U_0}{2}[H(j\omega)-H(-j\omega)]s+\dfrac{U_0}{2}\omega[H(j\omega)+H(-j\omega)]}{s^2+\omega^2} \end{matrix} \end{split}\]

escribiendo

\[ H(j\omega) = |H(j\omega)| e^{j \phi(\omega)} \]

con \(\phi (\omega)=\angle{H(j\omega)}\)

por lo que:

\[\begin{split} \begin{matrix} (1)&=& \dfrac{-jU_0 |H(j\omega)| s\dfrac{\big(e^{j \phi(\omega)}-e^{-j \phi(\omega)}\big)}{2} +U_0\omega|H(j\omega)|\dfrac{\big(e^{j \phi(\omega)}+e^{-j \phi(\omega)}\big)}{2} }{s^2+\omega^2}\\ &=& U_0 |H(j\omega)| \left[\dfrac{s}{s^2+\omega^2} \sin(\phi(\omega))+\dfrac{\omega}{s^2+\omega^2}\cos(\phi(\omega))\right] \end{matrix} \end{split}\]

tomando la transformada inversa de \(Y(s)\) se obtiene

\[ y(t)= \sum_{i=1}^n{\alpha_i e^{p_i t}} +U_0 |H(j\omega)| \left[\cos(\omega t) \sin(\phi(\omega))+\sin(\omega t)\cos(\phi(\omega))\right] \]

Lo anterior se puede escribir como:

\[ y(t)= \sum_{i=1}^n{\alpha_i e^{p_i t}} +\underbrace{U_0 |H(j\omega)| \sin(\omega t+\phi(\omega))}_{\text{Forzada}} \]

asumiendo que el sistema es BIBO estable, entonces

\[ p_1,p_2,\cdots, p_n < 0 \]

y el término de la respuesta transitoria

\[ \sum_{i=1}^n{\alpha_i e^{p_i t}} \longrightarrow 0 \text{ con } t\longrightarrow \infty \]

Es decir, cuando \(t\longrightarrow \infty\) el sistema alcanza un régimen permanente senoidal (RPS) de la forma

\[ y_{RPS}(t)=\underbrace{U_0 |H(j\omega)| \sin(\omega t+\phi(\omega))}_{\text{Forzada}} \]

Notar que:

• La salida es una senoide de la misma frecuencia que la senoide de la entrada, amplificada o atenuada por \(|H(j\omega)|\) y desfasada por el ángulo \(\angle{H(j\omega)}\)

• al término

\[ H(j\omega) \equiv \left.H(s)\right|_{s=j\omega} \]

se lo llama Transferencia Armónica o respuesta en Frecuencia del sistema. Su conocimiento para todo \(\omega\) permite determinar la respuesta en régimen permanente a entradas sinusoidales

\[\begin{split} \begin{matrix} |H(j\omega)| \longrightarrow \text{ Amplitud}\\ \angle{H(j\omega)} \longrightarrow \text{ Fase} \end{matrix} \end{split}\]

Los resultados se pueden extender al caso de tener polos complejos conjugados y con multiplicidad. Siempre con la condición que sean estables, es decir \(\mathbb{Re}(p_i)<0\)

Diagrama de Bode

Lo que se hace normalmente es graficar la respuesta frecuencial del sistema. Para esto se usa que:

\[ H(\omega) = \underbrace{|H(\omega)|}_{\text{módulo}} e^{j\angle{H(\omega)}} \]

\(|H(\omega)|\) es el módulo de \(H(\omega)\) y \(\angle{H(\omega)}\) es el argumento.

Se suele graficar la respuesta de \(H(\omega)\) en diagramas logarítmicos de amplitud y fase.

\[\begin{split} \begin{matrix} |H(j\omega)|_{dB} = 20 \log{|H(j\omega)|} & \text{vs}&\log{w}\\ \angle{H(j\omega)} &\text{vs}&\log{w} \end{matrix} \end{split}\]

Sin perder generalidad podremos considerar que \(p_i\) y \(z_j\) son reales por lo que:

\[ G(s)= k \dfrac{\prod_{j=1}^{m}(\tau_{z_j}s+1)}{\prod_{i=1}^{n}(\tau_{p_i}s+1)} \]

expresado como la función transferencia armónica:

\[ H(\omega)= k \dfrac{\prod_{j=1}^{m}(j\tau_{z_j}\omega+1)}{\prod_{i=1}^{n}(j\tau_{p_i}\omega+1)}= k \dfrac{\prod_{j=1}^{m}r_{z_j}e^{j\theta_{z_j}}}{\prod_{i=1}^{n}r_{p_i}e^{j\theta_{p_i}}} \]

con lo que:

\[ |G(j\omega)| = \dfrac{k\prod_{j=1}^{m}r_{z_j}(\omega)}{\prod_{i=1}^{n}r_{p_i}(\omega)} \]

\[ \angle{G(j\omega)} = e^{j\big(\sum_{j}^{m}\theta_{z_j}(\omega)-\sum_{i}^{n}\theta_{p_i}(\omega)\big)} \]

Finalmente, por propiedades de los logaritmos, el módulo en dB se determina sumando los módulos individuales de los polos y ceros para cada frecuencia.

\[ |G(j\omega)| = \underbrace{|k|_{dB}}_{20\log{(k)}} + \underbrace{\sum_{1}^{m} r_{z_j}(\omega)}_{20\log{\big(r_{z_j}(\omega)\big)}} + \underbrace{\sum_{1}^{n} \dfrac{1}{r_{p_i}(\omega)}}_{20\log{\big(\dfrac{1}{r_{p_i}(\omega)}}\big)} \]

y la fase se obtiene sumando las fases de los polos y ceros en forma individual para cada frecuencia w.

\[ \angle{G(j\omega)} = \angle{k} +\sum{\theta_{z_j}(\omega)}- \sum{\theta_{p_i}(\omega)} \]

El resultado anterior nos permite graficar un diagrama de Bode a partir de diagramas de Bode de sistemas mas simples. Analizaremos cada una de estas opciones tanto para polos como para ceros.

Método práctico para graficar diagramas de Bode

1) Polo simple en el origen

\[ \begin{matrix} G(s)=\dfrac{1}{s} & H(\omega)= \dfrac{1}{j\omega} & \text{polo en} & s=0 \end{matrix} \]

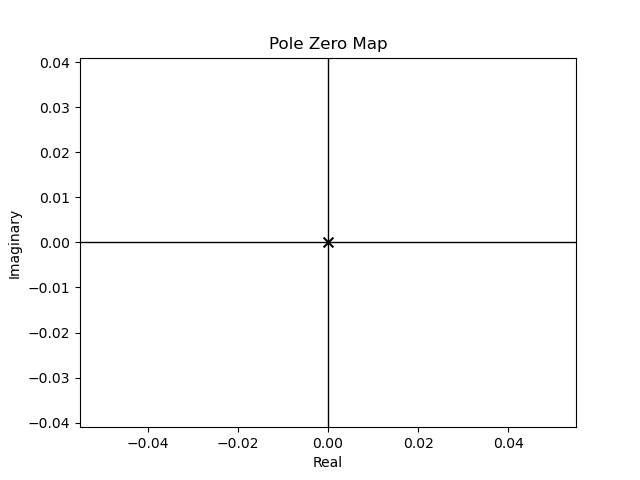
Figura 55 Polo en 0

el módulo resulta

\[\begin{split} |G(j\omega)| = \dfrac{1}{\omega} \Longrightarrow \underbrace{|G(j\omega)|_{dB} = - 20 \log{\omega}}_{\substack{\text{Ecuación de una recta}\\ \text{con pendiente de -20dB/dec}\\ \text{(con } \omega \text{ en forma logarítmico)}}} \end{split}\]

para frecuencia \(\omega = 1 \dfrac{rad}{seg}\) tenemos que el módulo es:

\[ |G(j\omega)|_{\omega = 1 \dfrac{rad}{seg}} = 0 dB \]

y la fase resulta

\[ \angle{G(j\omega)} = -\dfrac{\pi}{2} ~\forall~ \omega \]

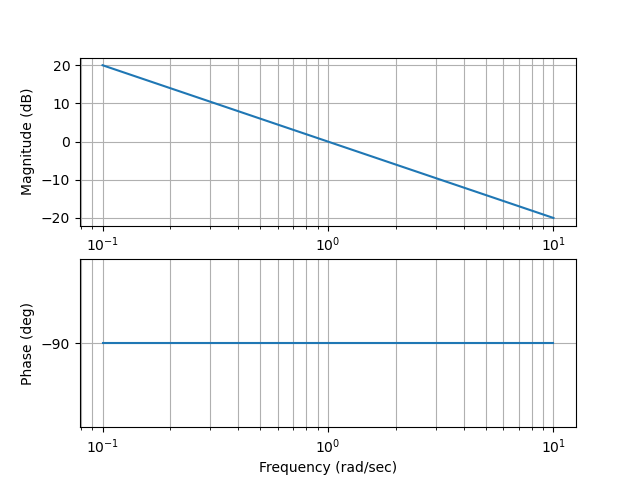
Figura 56 Bode de \(G(s)=\dfrac{1}{s}\)

2) Polo múltiple en el origen

\[ \begin{matrix} G(s)=\dfrac{1}{s^n} & G(j\omega)= \dfrac{1}{j^n\omega^n} & \text{n polos en} & s=0 \end{matrix} \]

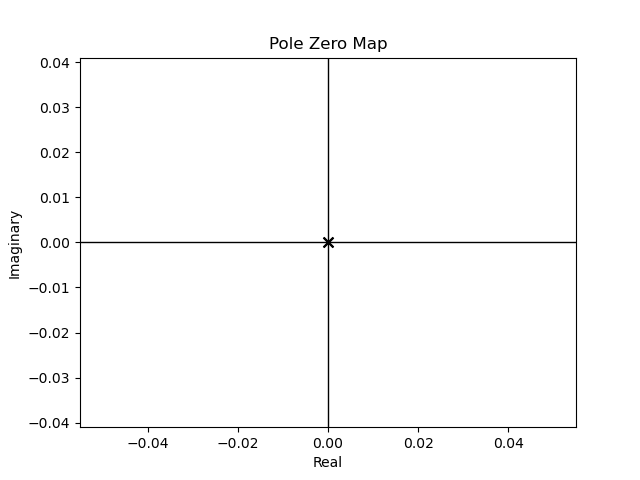
Figura 57 Polos de \(G(s)\) en \(s=0\) de multiplicidad \(n\)

el módulo resulta

\[\begin{split} |G(j\omega)| = \dfrac{1}{\omega^n} \Longrightarrow |G(j\omega)|_{dB} = \underbrace{-20~n}_{ \substack {\text{Solo cambia la pendiente en función}\\ \text{de la multiplicidad "n"}} }\log{\omega} \end{split}\]

para frecuencia \(\omega = 1 \dfrac{rad}{seg}\) tenemos que el módulo es:

\[ |G(j\omega)|_{\omega = 1 \dfrac{rad}{seg}} = 0 dB \]

y la fase resulta

\[ \angle{G(j\omega)} = -n \dfrac{\pi}{2} ~\forall~ \omega \]

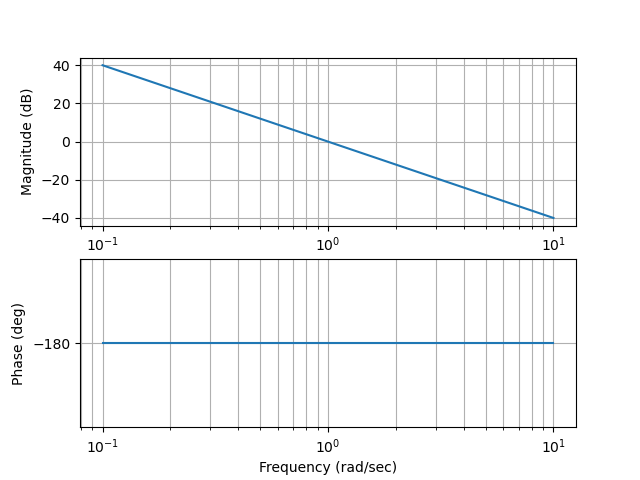
Figura 58 Bode cuando n=2, es decir \(G(s)=\dfrac{1}{s^2}\)

3) Polo real simple

\[ \begin{matrix} G(s)=\dfrac{1}{\tau s+1} & H(\omega)= G(j\omega)= \dfrac{1}{j\omega\tau+1} & \text{polo en} & s=-\dfrac{1}{\tau} \end{matrix} \]

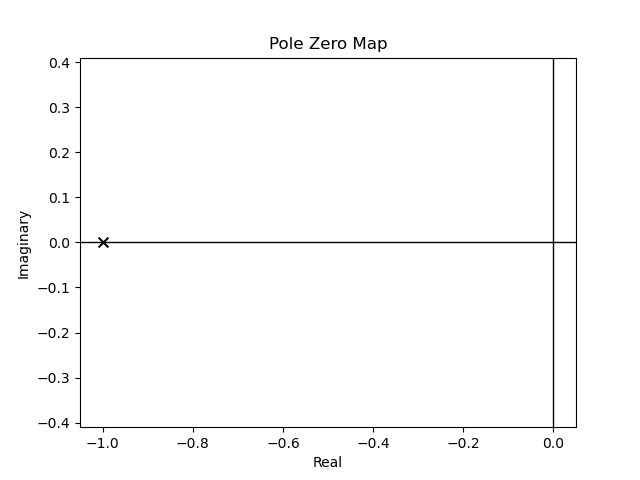
Figura 59 Polo de \(G(s)\) en \(s=-1/\tau\)

el módulo resulta

\[ |G(j\omega)| = \dfrac{1}{\sqrt{1+\omega^2\tau^2}} \Longrightarrow |G(j\omega)|_{dB} = - 10 \log{(1+\omega^2\tau^2)} \]

cuando \(\omega \longrightarrow 0\) el módulo se puede aproximar a la asíntota:

\[ |G(j\omega)|_{dB} \approx 0 dB \]

para \(\omega \longrightarrow \infty\) el módulo puede aproximarse a la asíntota:

\[\begin{split} |G(j\omega)|_{dB} \approx -10 \log(\omega^2\tau^2) = \underbrace{-20\log(\omega)-20\log(\tau)}_{\substack {\text{Ecuación de una recta}\\ \text{con pendiente -20dB/dec}\\ \text{que corta el eje}\\ \text{en 0 dB para } \omega=\dfrac{1}{\tau} }} \end{split}\]

Notar que para \(\omega=\dfrac{1}{\tau}\) el módulo es:

\[ {|G(j\omega)|_{dB}}_{\omega=\dfrac{1}{\tau}} = -10 \log(1+1) = -3dB \]

la fase resulta ser:

\[\begin{split} \angle{G(j\omega)} = \arctan(-\omega\tau)= \left\{ \begin{array}{l} \angle{G(j\omega)} \rightarrow 0 \text{ cuando } \omega\rightarrow 0 \\ \angle{G(j\omega)} \rightarrow -\dfrac{\pi}{2} \text{ cuando }\omega\rightarrow\infty \\ \left.\angle{G(j\omega)}\right|_{\omega=\dfrac{1}{\tau}} = -\dfrac{\pi}{4} \end{array}\right. \end{split}\]

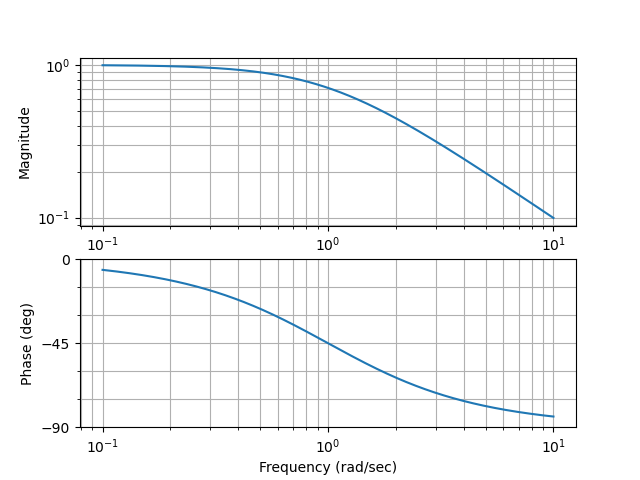
Figura 60 Bode de \(G(s)=\dfrac{1}{\tau s+1}\) con \(\tau=1\)

4) Par de polos complejo conjugado

\[ G(s)=\dfrac{\omega_n^2}{s^2+2\xi\omega_ns+\omega_n^2} \]

donde \(\xi\) es el coeficiente de amortiguamiento, \(\omega_n\) es la frecuencia natural y los polos se ubican en \(\underbrace{p_{1,2}=-\xi\omega_n\pm \omega_n\sqrt{\xi^2-1}}_{\text{complejos conjugados}}\) para \(0<\xi<1\) y \(|p_{1,2}|=\omega_n\)

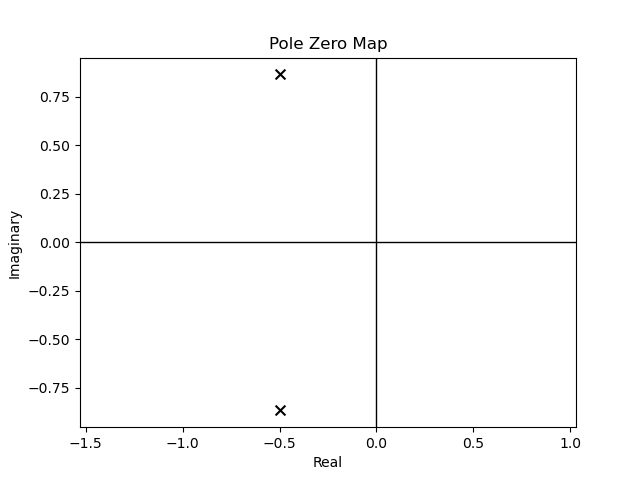
Figura 61 Polo complejos conjugados de \(G(s)\) con \(\omega_n=1\) y \(\xi=0.5\)

\[ H(\omega)= G(j\omega)= \dfrac{\omega_n^2}{-\omega_n^2+j2\xi\omega_n\omega+\omega_n^2} =\dfrac{1}{\big(1-\dfrac{\omega^2}{\omega_n^2}\big)+j2\xi\dfrac{\omega}{\omega_n}} \]

el módulo es

\[ |G(j\omega)| = \dfrac{1}{\sqrt{\big(1-\dfrac{\omega^2}{\omega_n^2}\big)^2+4\xi^2\dfrac{\omega^2}{\omega_n^2}}} \]

\[ \left.|G(j\omega)|\right|_{dB} = -10\log\left(\left(1-\dfrac{\omega^2}{\omega_n^2}\right)^2+4\xi^2\dfrac{\omega^2}{\omega_n^2}\right) \]

cuando \(\omega \longrightarrow 0\) el módulo se puede aproximar a la asíntota:

\[ |G(j\omega)|_{dB} \approx 0 dB \]

y para \(\omega \longrightarrow \infty\) el módulo puede aproximarse a la asíntota:

\[\begin{split} |G(j\omega)|_{dB} \approx -10 \log\big(\dfrac{\omega^4}{\omega_n^4}\big) = \underbrace{-40\log(\omega)+40\log(\omega_n)}_{\substack {\text{Ecuación de una recta}\\ \text{con pendiente -40dB/dec}\\ \text{que corta el eje}\\ \text{en 0 dB para } \omega=\omega_n }} \end{split}\]

El módulo para \(\omega=\omega_n\) es:

\[ {|G(j\omega)|_{dB}}_{\omega=\omega_n} = -10 \log(4\xi^2) = -6dB -20\log(\xi) \]

la fase es:

\[\begin{split} \angle{G(j\omega)} = \arctan\bigg(-\dfrac{2\xi\dfrac{\omega}{\omega_n}}{(1-\dfrac{\omega^2}{\omega_n^2})}\bigg)= \left\{ \begin{array}{l} \rightarrow 0 \text{ cuando } \omega\rightarrow0\\ \rightarrow -\pi \text{ cuando } \omega\rightarrow\infty\\ = -\dfrac{\pi}{2} \text{ para } \omega=\omega_n \end{array}\right. \end{split}\]

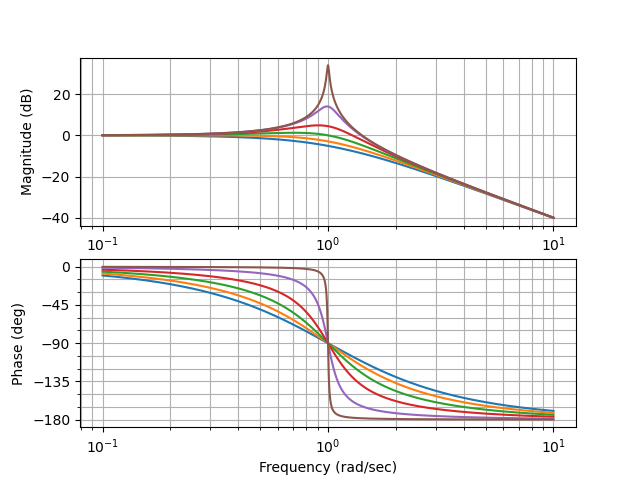
Figura 62 Bode de \(G(s)\) con \(\omega_n=1\) y \(\xi= 0.9,0.7,0.5,0.3,0.1,0.01\)

5) Cero simple en el origen

\[ \begin{matrix} G(s)=s & H(\omega)= {j\omega} & \text{un cero en} & s=0 \end{matrix} \]

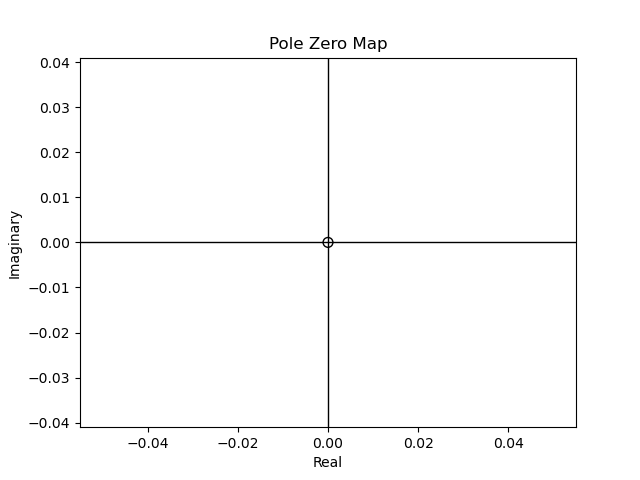
Figura 63 Cero de \(G(s)\) en \(s=0\)

el módulo resulta

\[\begin{split} |G(j\omega)| = {\omega} \Longrightarrow \underbrace{|G(j\omega)|_{dB} = 20\log{\omega}}_{\substack{\text{recta con}\\ \text{pendiente de 20dB/dec}}} \end{split}\]

para

\[ |G(j\omega)|_{\omega = 1 \dfrac{rad}{seg}} = 0 dB \]

la fase \(\angle{G(j\omega)} = \dfrac{\pi}{2} ~\forall~ \omega\)

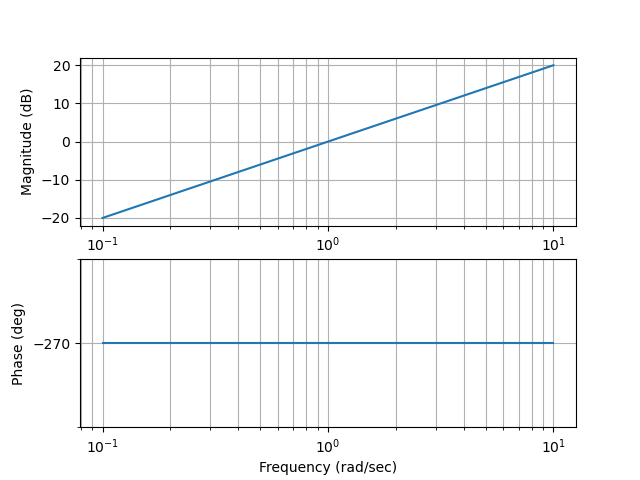
Figura 64 Bode de \(G(s)={s}\)

6) Ceros múltiples en el origen

\[ \begin{matrix} G(s)={s^n} & G(j\omega)= {j^n\omega^n} & \text{n ceros en} & s=0 \end{matrix} \]

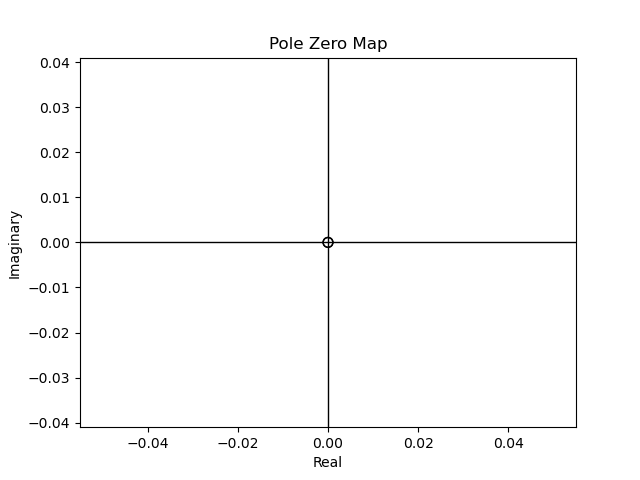
Figura 65 Ceros de \(G(s)\) en \(s=0\) de multiplicidad n

el módulo resulta

\[\begin{split} |G(j\omega)| = {\omega^n} \Longrightarrow \underbrace{|G(j\omega)|_{dB} = 20~n\log{\omega}}_{ \substack {\text{Solo cambia la pendiente en función}\\ \text{de la multiplicidad "n"}} } \end{split}\]

sigue valiendo \(|G(j\omega)|_{\omega = 1 \dfrac{rad}{seg}} = 0 dB\)

y la fase resulta

\[ \angle{G(j\omega)} = n \dfrac{\pi}{2} ~\forall~ \omega \]

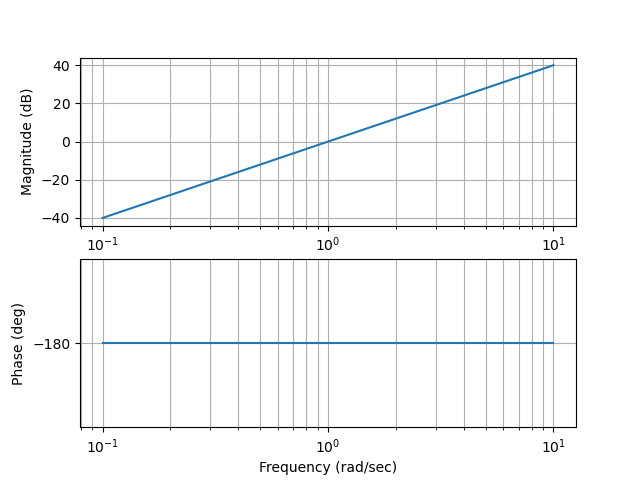
Figura 66 Bode cuando n=2, es decir \(G(s)={s^2}\)

7) Cero real simple

\[ \begin{matrix} G(s)={\tau s+1} & H(\omega)= G(j\omega)= {j\omega\tau+1} & \text{un cero en} & s=-\dfrac{1}{\tau} \end{matrix} \]

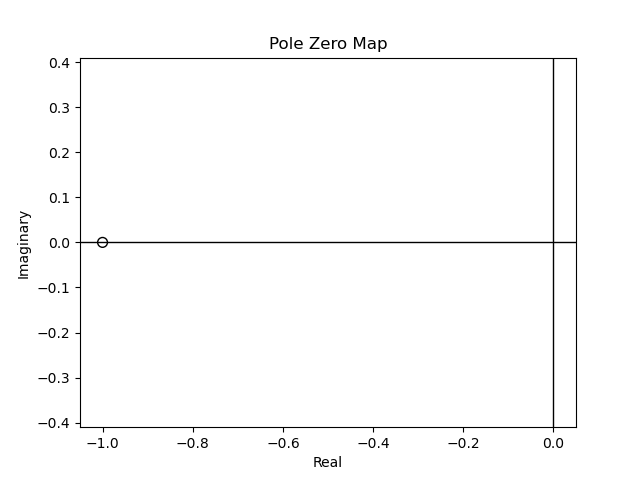
Figura 67 Cero de \(G(s)\) en \(s=-1/\tau\)

el módulo resulta

\[ |G(j\omega)| = {\sqrt{1+\omega^2\tau^2}} \Longrightarrow |G(j\omega)|_{dB} = 10\log{(1+\omega^2\tau^2)} \]

cuando \(\omega \longrightarrow 0\) el módulo se puede aproximar a la asíntota:

\[ |G(j\omega)|_{dB} \approx 0 dB \]

para \(\omega \longrightarrow \infty\) el módulo puede aproximarse a la asíntota:

\[\begin{split} |G(j\omega)|_{dB} \approx 10\log(\omega^2\tau^2) = \underbrace{20\log(\omega)+20\log(\tau)}_{\substack {\text{Ecuación de una recta}\\ \text{con pendiente 20dB/dec}\\ \text{que corta el eje}\\ \text{en 0 dB para } \omega=\dfrac{1}{\tau} }} \end{split}\]

para \(\omega=\dfrac{1}{\tau}\) el módulo es:

\[ {|G(j\omega)|_{dB}}_{\omega=\dfrac{1}{\tau}} = 10\log(2) = 3dB \]

la fase resulta ser:

\[\begin{split} \angle{G(j\omega)} = \arctan(\omega\tau)= \left\{ \begin{array}{l} \rightarrow 0 \text{ cuando } \omega\rightarrow0\\ \rightarrow \dfrac{\pi}{2} \text{ cuando } \omega\rightarrow\infty\\ =\dfrac{\pi}{4}\text{ con }\omega=\dfrac{1}{\tau} \end{array}\right. \end{split}\]

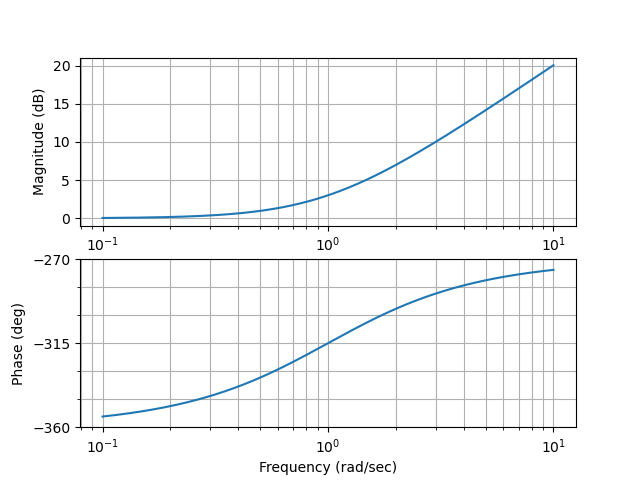
Figura 68 Bode de \(G(s)={\tau s+1}\) con \(\tau=1\)

8) Cero complejo conjugado

De forma similar a lo resuelto para los polos complejos conjugados, se puede llegar a que la respuesta en frecuencia de la siguiente función de transferencia con un para de ceros complejos conjugados normalizada en ganancia, es:

\[ G(s)=\dfrac{s^2+2\xi\omega_ns+\omega_n^2}{\omega_n^2} \]

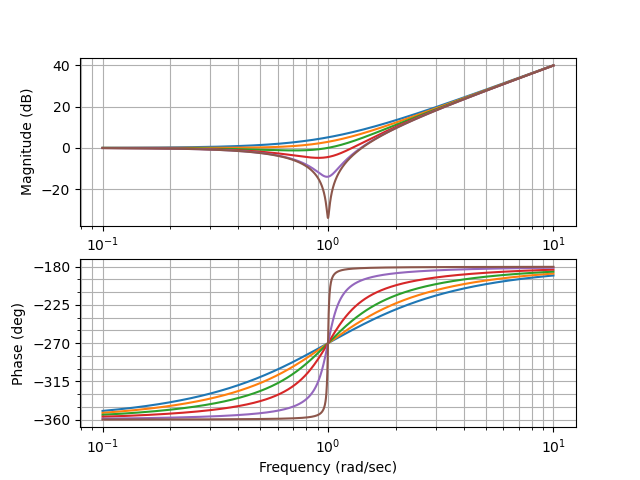
Figura 69 Bode de \(G(s)\) con \(\omega_n=1\) y \(\xi= 0.9,0.7,0.5,0.3,0.1,0.01\)

9) Cero simple de no mínima fase

\[ \begin{matrix} G(s)={1-\tau s} & H(\omega)= G(j\omega)= {1-j\omega\tau} & \text{un cero en } & s=\dfrac{1}{\tau} \end{matrix} \]

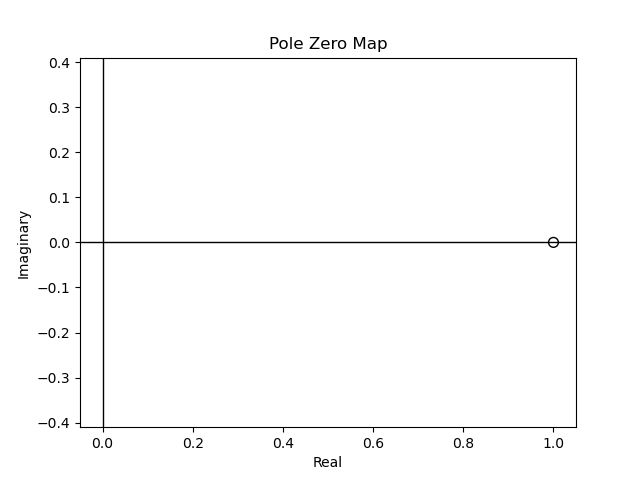
Figura 70 Cero de \(G(s)\) en \(s=1/\tau\), en \(\mathbb{C}^+\)

el módulo resulta

\[ |G(j\omega)| = {\sqrt{1+\omega^2\tau^2}} \Longrightarrow |G(j\omega)|_{dB} = 10\log{(1+\omega^2\tau^2)} \]

cuando \(\omega \longrightarrow 0\) el módulo se puede aproximar a la asíntota:

\[ |G(j\omega)|_{dB} \approx 0 dB \]

para \(\omega \longrightarrow \infty\) el módulo puede aproximarse a la asíntota:

\[\begin{split} |G(j\omega)|_{dB} \approx 10\log(\omega^2\tau^2) = \underbrace{20\log(\omega)+20\log(\tau)}_{\substack {\text{Una recta con}\\ \text{pendiente 20dB/dec}\\ \text{al igual que para}\\ \text{el cero en } \mathbb{C}^- }} \end{split}\]

para \(\omega=\dfrac{1}{\tau}\) el módulo es:

\[ {|G(j\omega)|_{dB}}_{\omega=\dfrac{1}{\tau}} = 10\log(2) = 3dB \]

la fase resulta ser:

\[\begin{split} \angle{G(j\omega)} = \arctan(-\omega\tau)= \left\{ \begin{array}{l} \rightarrow 0 \text{ cuando } \omega\rightarrow0\\ \rightarrow -\dfrac{\pi}{2} \text{ cuando } \omega\rightarrow\infty\\ =-\dfrac{\pi}{4}\text{ con }\omega=\dfrac{1}{\tau} \end{array}\right. \end{split}\]

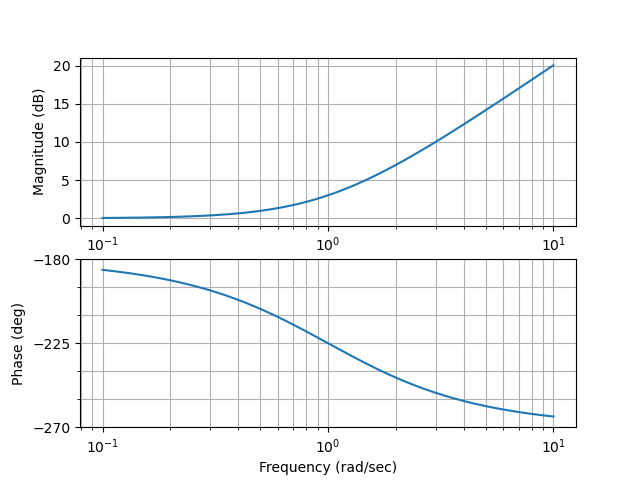
Figura 71 Bode de \(G(s)={1-\tau s}\) con \(\tau=1\)

Pasos para dibujar un diagrama de Bode

1. Manipular la función de transferencia \(G(s)\) para que quede de la forma:

\[ G(s)= k_0 \dfrac{\prod_{j=1}^{m}(\tau_{j}s+1)}{\prod_{i=1}^{n}(\tau_{i}s+1)} \]

1. Magnitud: Determinar las singularidades en el origen \(\Longrightarrow k_0(j\omega)^n\) (resultado de los polos y/o ceros de multiplicidad n) Graficar la asintota en baja frecuencia (\(n~x~20dB/dec\)) y calcular la magnitud de \(k_0\) a \(\omega = 1\)

2. Completar la magnitud extender las asintotas para bajas frecuencias hasta el primer punto de quiebre \(\Longrightarrow\) cambiar la pendiente en función del orden del o los polos y/o ceros de primer orden o segundo orden.

3. Dibujar el módulo aproximado sabiendo que los polos/ceros en el punto de quiebre, modifican en -3dB/3dB respectivamente y para los polos/ceros de segundo orden \(\Longrightarrow |G(j\omega)|_{dB} \approx \dfrac{1}{2}\xi\)

4. Graficar asintotas en baja frecuencia como \(\phi = n~90º\)

5. Aproximar como guía con saltos de \(\pm 90º\) para primer orden y \(\pm 180º\) para segundo orden en los puntos de quiebre de magnitud

6. Aproximar con una asintota el salto según corresponda

7. Se puede aproximar por una curva suave en forma aproximada.

Ejemplo: Primer Bode asintótico

Seguimos los pasos anteriores para dibujar un Bode asintótico

\[ G(s) = \dfrac{200(s+0.5)}{s(s+10)(s+50)} \]

1. step) reescribir la FT de la forma:

\[ H(\omega)=G(j\omega) = \dfrac{0.2(\dfrac{j\omega}{0.5}+1)}{j\omega~\big(0.1j\omega+1\big)\big(\dfrac{j\omega}{50}+1\big)} \]

2. step) para bajas frecuencias tenemos que:

\[ \begin{matrix} G(j\omega) \simeq \dfrac{0.2}{j\omega} & -20dB/dec & \text{ para } & \omega \longrightarrow 0 \end{matrix} \]

para \(\omega = 1 \Longrightarrow k_0=0.2 \Longrightarrow \approx -14dB\)

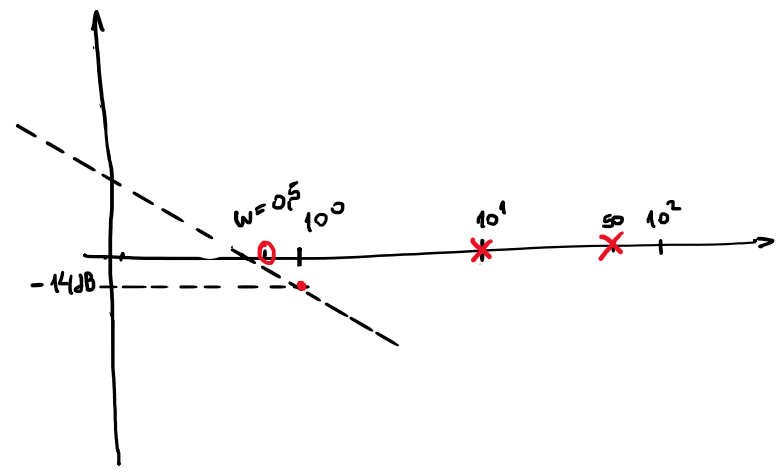
3. step) Dibujar las asíntotas

\[\begin{split} \text{puntos de quiebres } \omega = \left\{ \begin{array}{l} 0.5 \text{ (un cero) la pendiente pasa a } 0dB/dec \simeq -8dB\\ 10 \text{ (un polo) la pendiente pasa a } -20dB/dec \\ 50 \text{ (un polo) la pendiente pasa a } -40dB/dec \\ \end{array}\right. \end{split}\]

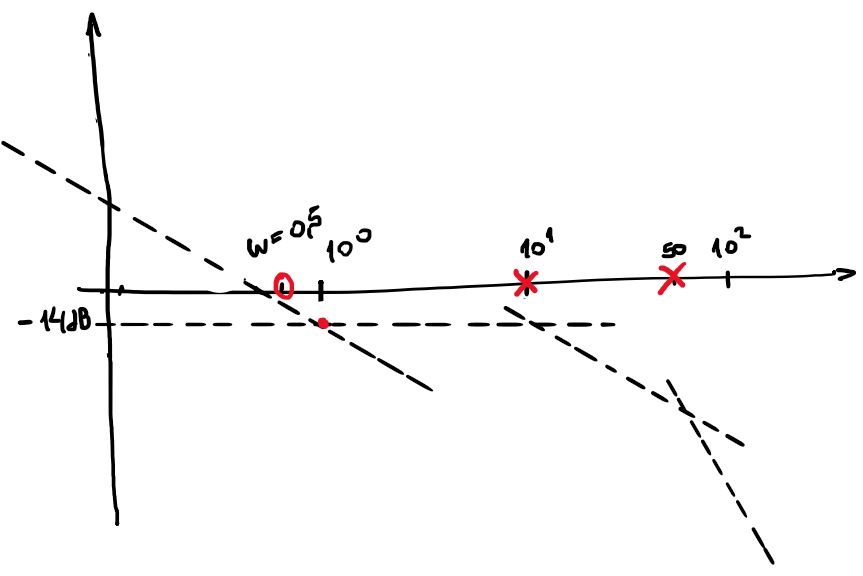
4. step) corrección del módulo en los puntos de quiebre

\[\begin{split} \text{puntos de quiebres } ||_{dB} = \left\{ \begin{array}{l} +3dB \text{ para } \omega = 0.5\\ -3dB \text{ para } \omega = 10\\ -3dB \text{ para } \omega = 50\\ \end{array}\right. \end{split}\]

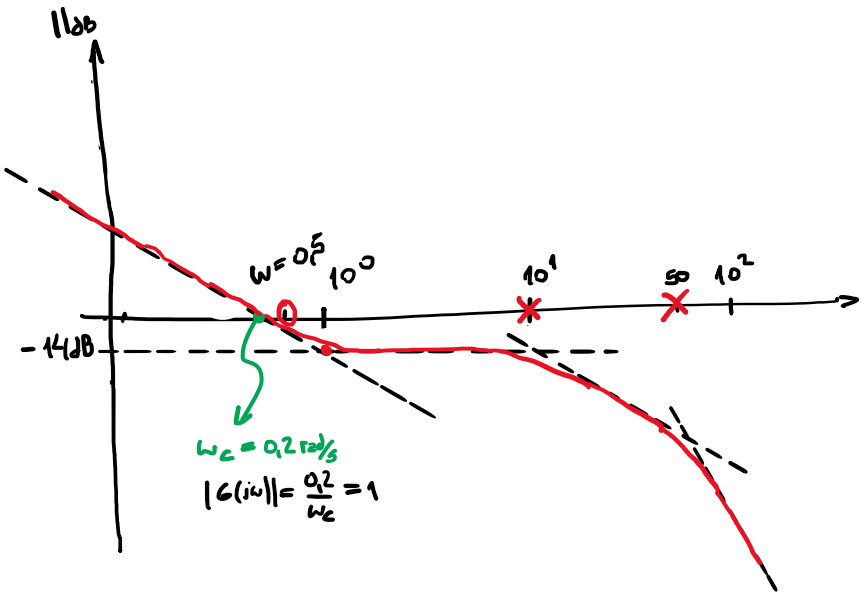
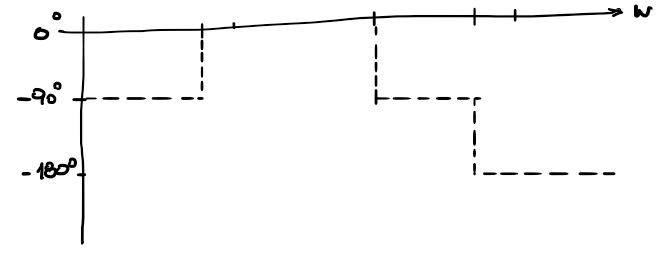
5. step) Fase a baja frecuencia el \(-90º\)

6. step) Graficar escalones en puntos de equilibrio

7. step) dibujar asíntotas, en verde la asintotas con una recta en +/- media decada.

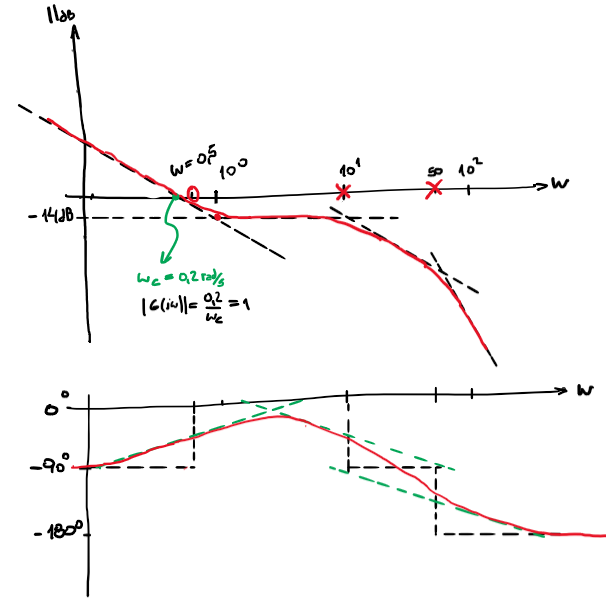
Figura 72 Bode asintótico

Ejemplo:

Graficaremos el Bode asintótico de la siguiente función de transferencia

\[ G(s)=5\dfrac{\dfrac{1}{2}s+1}{(s+1)(10s+1)} \]

La frecuencia de corte por 0dB se calcula

\[ \underbrace{|G(j\omega)|_{\omega=\omega_c}=5\dfrac{|\dfrac{1}{2}j\omega+1|}{|j\omega+1||10j\omega+1|}=1}_{\omega_c = 0.456 rad/s} \]

Figura 73 Bode asintótico de \(G(s)\)